Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/04/2024 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Quart de cercle	Deux cercles et rectangle
	Fourmi sur un pavé	Cinq cercles (arbelos)	Trois cercles tangents
	Cercle sur équerre	Cercle et trois points	Quatre cercles et un quart

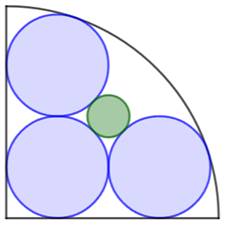
Quatre cercles dans un quart de cercle Quelle est la ralation entre les rayons des cercles ?
	Sommaire de cette page >>> Rayon du petit cercle	Débutants Géométrie Glossaire Géométrie

Rayon du petit cercle		haut
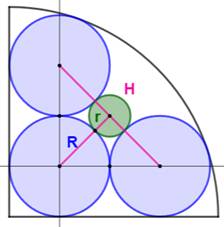
Construction Trois cercles tangents deux à deux et tangents à un quart de cercle. Un quatrième cercle est tangent aux trois cercles comme l'indique la figure. Quelle est la relation entre les rayons r et R ? Piste Une fois les tracés complémentaires réalisés, on met en évidence un triangle rectangle (qui est même isocèle). On est tenté d'appliquer le théorème de Pythagore. On obtient une expression reliant les rayons R et r dont on tirera r en fonction de R. Deux méthodes La première (brutale) consiste à écrire la relation complète qui s'avère être du second degré. Sa résolution est simple. La deuxième méthode consiste à passer par le relais de l'hypoténuse H. Alors, on évite l'équation du second degré.	Figure de l'énoncé Figure avec notations
Calculs

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Nappe sur table Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/TroiCerc.htm