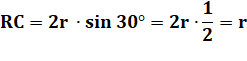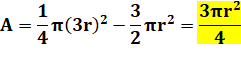Cercle dans un quart de cercle et avec demi-cerle

Édition du: 08/10/2024

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Quart de cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Défis divers
	Trois triangles réunis	Cercle et demi-cercle	Cercle et quart de cercle
			Demi-cercle – Divers

Cercles dans le quart-cercle

Demi- cercle et cercle internes à un quart de cercles.
Deux énigmes classiques.

Sommaire de cette page

>>> Le cercle dans le quart de cercle

>>> Un cercle et demi dans un quart de cercle

>>> Sécante sur cercle et demi cercle

Débutants

Géométrie

Glossaire

Géométrie

Le cercle dans le quart de cercle

haut

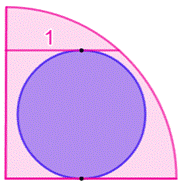
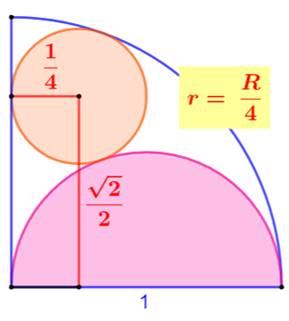
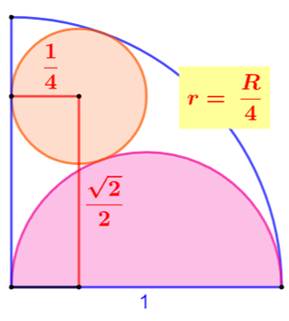
Construction

Un quart de cercle et un demi-cercle construit sur le rayon du premier.

Un cercle prend place dans l'espace libre tout en étant tangent aux deux cercles et à un côté du quart de cercle.

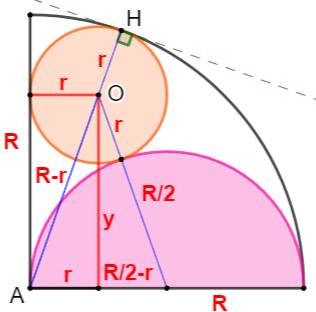
Montrer que le rayon du petit cercle est égal au quart du rayon du plus grand cercle.

Piste (Figure du bas)

Se rappeler que le rayon qui rejoint un point de tangence est perpendiculaire à la tangente.

Dans le quart de cercle, le rayon AH est perpendiculaire à la tangente verte.

Dans le petit cercle, le rayon OH est perpendiculaire à la tangente verte.

Conclusion; A, O et H sont alignés.
Alors, AH = R et AO = R – r

Calculs ave le théorème de Pythagore

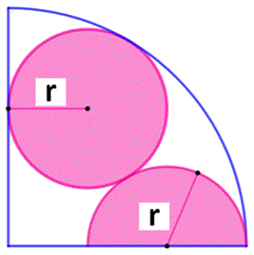
Un cercle et demi dans un quart de cercle

haut

Construction

Un quart de cercle.

Un demi-cercle de rayon r dont le diamètre est sur un côté du quart de cercle.

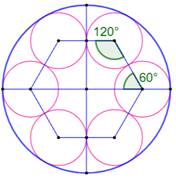
Un cercle complet de même rayon r occupe l'espace libre. Il est tangent aux deux cercles existants et à un côté du quart de cercle.

Quelle est l'aire de la surface blanche ?

Angles (Figure du milieu)

Cette figure complétée des trois autres quarts de cercles montre que les centres des cercles sont les sommets d'un hexagone.

On retient la valeur des angles.

Points R et S (Figure du bas)

On joint le point O au point S, extrémité du demi-cercle.

On trace également la perpendiculaire OR en O au côté du quart de cercle.

On se propose de montrer que les points R et S sont confondus.

Par construction l'angle KOR est droit. Or l'angle de l'hexagone vaut 120°. Alors, l'angle ROC vaut 30°.

Évaluation du segment RC par l'intermédiaire du sinus de cet angle:

Le point R est bien confondu avec le point S.

De sorte que le rayon du quart de cercle est 3r.

Aire de la surface blanche

Aire du quart de cercle moins un petit cercle et demi.

L'aire de la surface blanche est équivalente à 3/4 de celle du petit cercle.

Sécante sur cercle et demi cercle

haut

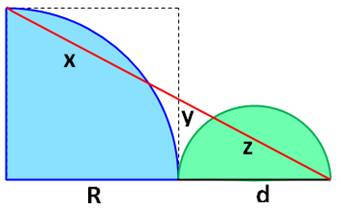
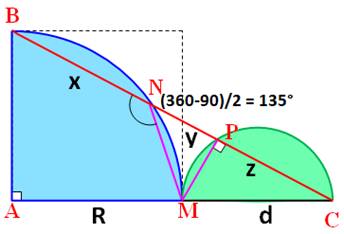
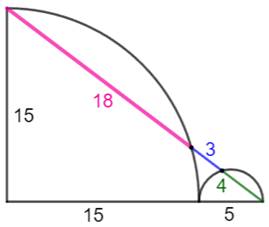
Construction

Un quart de cercle et un demi-cercle alignés sur le diamètre du demi-cercle.

Une sécante traverse ces deux portions de cercle et les découpe selon les longueurs x, y et z.

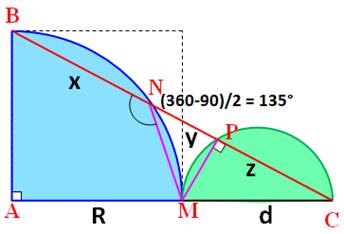
Quelle est la relation x en fonction de y et z avec y = 3 et z = 4 ?

Pistes (Figure du milieu)

Tracer les deux segments MN et MP.

Le triangle MPC est inscrit dans un demi-cercle, il est rectangle.

Moins facile à observer: l'angle BNM intercepte l'arc BM, le grand arc, l'arc majeur. Sa valeur est moitié de celle de l'angle au centre interceptant le même angle.

Or, l'angle au centre mesure 360° – 90° = 270°. L'angle inscrit BNM = 135°. Par suite, l'angle MNP vaut 180° – 135° = 45°

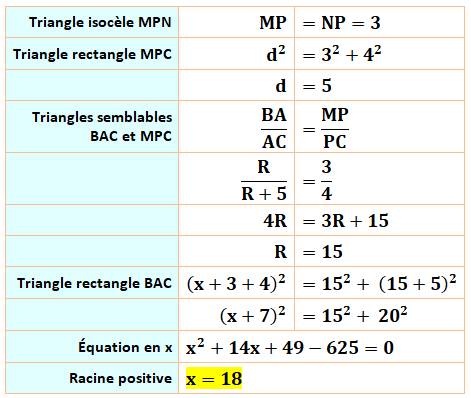
Dans le triangle rectangle MPN, un des angles vaut 45°, l'autre aussi; ce triangle est isocèle et MP = NP = y

Calculs

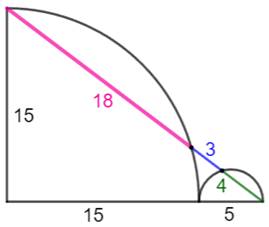
Figure de l'énoncé

Notations

Figure à l'échelle

Voir Triplets de Pythagore / Angle inscrit / Triangle semblables / Équation du second degré

Haut de page

Retour	Autres défis Géométrie – Index Énigmes – Index Brèves – Index
Suite	Quadrilatère dans le quart de cercle Divers défis 02 Équation en x⁴ Résolution LLL du triangle Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Site	104) A very interesting Q with short solution – Relish Maths
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CercleQD.htm