Rayon du quart de cercle inscrivant un triangle rectangle

Édition du: 28/07/2023

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Quart de cercle	Deux demi-cercles
	Cercle et trg rectangle	Quatre cercles et carré	Demi-cercle et rectangle
	Carré oblique	Trois cercles tangents	Trois triangles réunis
	Fourmi sur un pavé	Cercle et demi-cercle	Défis divers

Cercle et triangle rectangle

Un triangle rectangle inscrit dans un quart de cercle.
Quel est le rayon du cercle ?

Sommaire de cette page

>>> Cercle et triangle rectangle

Débutants

Géométrie

Glossaire

Géométrie

Cercle et triangle rectangle		haut
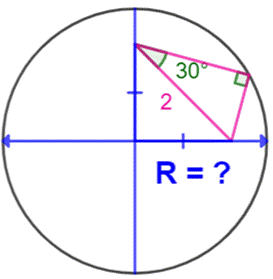
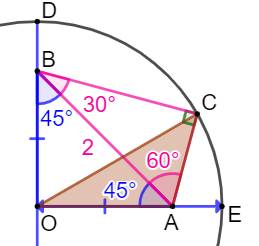
Construction Un cercle et un triangle rectangle inscrit dans le quart de cercle. Triangle rectangle: les sommets opposés à l'angle droit sont situés sur deux diamètres perpendiculaires et à égale distance du centre du cercle. Son hypoténuse mesure 2 cm et le petit angle vaut 30°. Quel est le rayon du cercle ? Observations liminaires (Figure du bas) Les segments OA et OB sont égaux. Le triangle OAB est isocèle rectangle. Son hypoténuse valant 2, les côtés mesurent racine de 2 (2² = x² + x² = 2x² => x² = 2). Dans le triangle rectangle ABC, on connait l'hypoténuse AB et l'angle de 30° (angle ABC), alors les deux côtés de l'angle droit sont connus (le sinus et le cosinus). Pistes Il faut calculer le rayon: R = OE = OD et aussi … OC. Le segment OC est situé parmi des triangles dont on connait les angles. Intuition: utilisation des formules d'Al Kashi (ou loi des cosinus avec un des triangles OCB ou OCA. Avec OCA, on connait l'angle en A et la mesure du côté OA. Peut-on calculer la longueur du segment AC ? Oui, avec le théorème de Pythagore dans le triangle rectangle ABC.
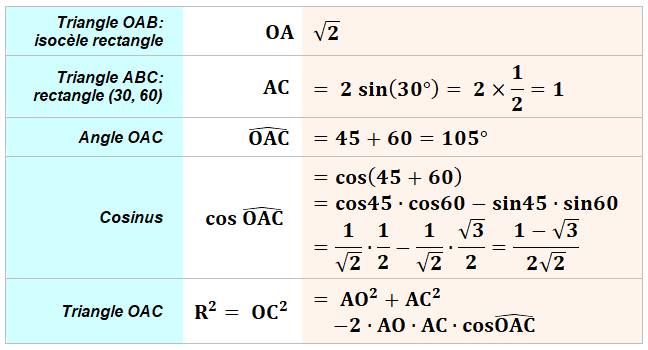
Calculs Notez la manière de s'affranchir d'un radical sous radical en mettant en évidence un carré.

D'après Find the radius of the quarter circle – Geometry Problem – Math Booster

Retour	Autres défis Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x⁴ Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CerQuTrg.htm