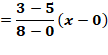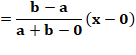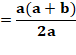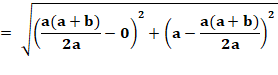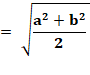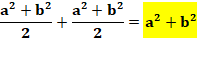|
Édition du: 19/12/2024 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
Quatre carrés Une
propriété un peu semblable au théorème
de Pythagore … |
||
|
|
Sommaire de cette page >>> Quatre carrés |
Débutants Glossaire |
|
Construction Deux carrés
accolés de côté a = 5 et b = 3. La diagonale du premier carré coupe l'oblique
joignant deux sommets des deux carrés. Un nouveau carré est construit comme indiqué et un quatrième prend la diagonale pour
côté. Montrer que la somme des aires des carrés bleu et
ocre vaut l'aire du carré vert (ici: 25 + 9 = 34). Pistes (Figure
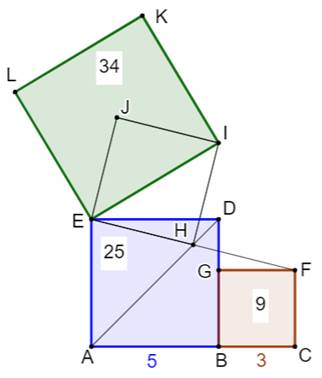
du bas) L'aire des carrés du bas est connue: a² + b². L'aire de celui du haut sera connue si on connait
le côté EI. Lequel sera déduit de la longueur de EH. Tout réside dans la connaissance du point H,
intersection de deux droites:
Cas numérique: a = 5 et b = 3
|
|
|||||||||||||||||||||||
|
Cas général
|
Dans le cas général, l'aire
des deux carrés du bas (a² + b²) est égale à celle du carré du haut. En numérique: 5² + 3² = 25 + 9 = 34 |
|||||||||||||||||||||||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/CarreQua.htm
|