Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 19/12/2024 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Carré et cercle	Deux demi-cercles
	Coin du carré replié	Quatre cercles et carré	Demi-cercle et rectangle
	Quatre carrés	Carré et triangle équil.	Trapèze et triangle
	Carré oblique	Carré et rectangle	Rectangles croisés
	Rectangle et deux cercles	Trois carrés plus un	Carré et 2 demi-cercles

Rectangle et deux cercles Comment déterminer la longueur du segment oblique ? Résolution en trois étapes: calcul du rayon du petit cercle, calcul des coordonnées des extrémités du segment et, enfin, calcul de la longueur du segment.
	Sommaire de cette page >>> Les deux cercles dans le rectangle	Débutants Géométrie Glossaire Géométrie

Les deux cercles dans le rectangle		haut
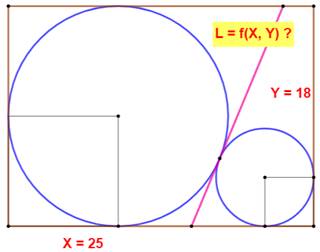
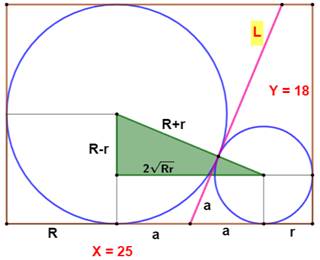
Construction Un rectangle (X = 25, Y = 15). Un grand cercle tangent à trois de côtés. Un petit cercle tangent à deux des côtés et au grand cercle. La tangente à ces deux cercles. Quelle est la longueur du segment de tangente inclus dans le rectangle ? Pistes Le rectangle vert réunissant les centres des cercles est calculable: Hypoténuse: R + r Petit côté: R – r Grand côté avec Pythagore: Les segments notés a sont des segments de tangentes issue du même point: ils ont même longueur. 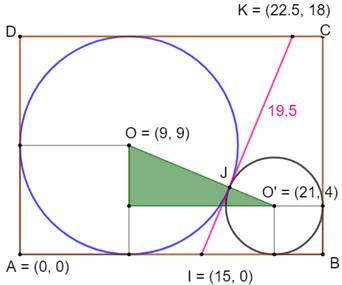Avec X la longueur du côté du rectangle: a = (X – R – r) / 2 En rapprochant: b = 2a et avec R = Y/2 = 9 36r = 16² – 32r + r² r² – 68r + 16² = 0 Seule compatible: r = 4 Et: Et aussi: a = (25 – 9 – 4) / 2 = 6 Calculs des coordonnées On note les coordonnées des points O, O', P et Q. Calcul de la pente de OO'; tangente de l'angle: m = – (R – r) / (R + r) = – (9 – 4) / 12 = –5/12 (pente négative) Pente de la droite PQ, perpendiculaire à OO': m' = – 1 / m = 12/5 Coordonnées du point Q: y – 0 = m' (x – (R+a)) 18 = 12/5 (x – 15) 12x = 90 + 180 => x = 45/2 = 22,5 Calculs de la longueur(Pythagore) IK² = (22,5 – 15)² + 18² = 380,25 IK = 19,5	Figure initiale Figure avec notations Figure pour calcul des coordonnées

Haut de page

Retour	Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Site	Inscribing two circles in a rectangle. A geometry puzzle – Vidéo en anglais de SyberMath
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/Carre2Ce.htm