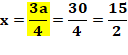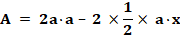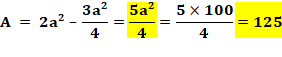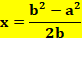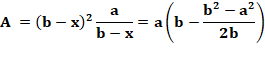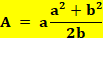|
Édition du: 08/12/2023 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
Rectangles croisés Deux
rectangles se croisent. Déterminer l'aire de la zone de recouvrement. |
||
|
|
Sommaire de cette page >>> Deux rectangles croisés >>> Deux rectangles croisés quelconques |
Débutants Glossaire |
|
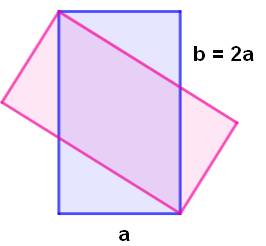
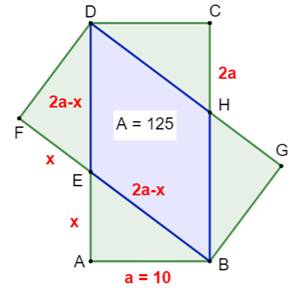
Construction Deux rectangles identiques se recouvrent comme
indiqué sur la figure. Leur longueur b vaut deux fois leur largeur a (par
exemple: a = 10). Quelle est l'aire du quadrilatère central, commun
aux deux rectangles ? Observations géométriques Les triangles EAB et DCH ont des angles
identiques deux à deux du fait des côtés parallèles des rectangles. Ils sont
semblables. Ils ont un côté de même longueur AB = DC. Ils sont isométriques
(égaux). Même chose pour les triangles EFD et HGB. Avec même angles et u côté de même mesure, les
quatre triangles verts sont isométriques. Alors, par exemple:
Valeur de x en fonction de a Théorème
de Pythagore dans un des triangles verts: a² + x² = (2a – x)² a² + x² = x² – 4ax +
4a² 4ax = 3a²
Aire du losange Aire losange = aire rectangle – 2 × aire triangle
|
Deux rectangles croisés
Notations
|
|
|
Construction Deux rectangles identiques se recouvrent comme
indiqué sur la figure. Largeur a et longueur b. Quelle est l'aire du quadrilatère central, commun
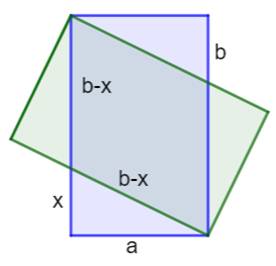
aux deux rectangles ? Observations géométriques Les mêmes que ci-dessus: le quadrilatère central
est un losange dot les côtés mesurent b – a. Valeur de x en fonction de a Théorème
de Pythagore dans un des triangles verts: a² + x² = (b – x)² a² + x² = x² – 2bx +
b² 2bx = b² – a²
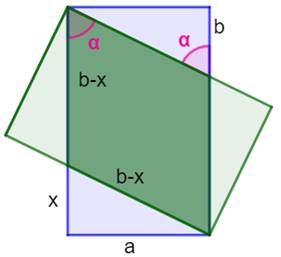
Aire du losange Aire
losange = (côté)² × sin α
|
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/RectCroi.htm
|