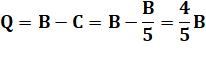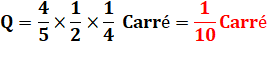énigme du carré flanqué de deux demi-cercles

Édition du: 19/12/2024

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Carré et cercle	Deux demi-cercles
	Coin du carré replié	Quatre cercles et carré	Demi-cercle et rectangle
	Quatre carrés	Carré et triangle équil.	Trapèze et triangle
	Carré oblique	Fourmi sur un pavé	Rectangles croisés
	Rectangle et deux cercles	Trois carrés plus un	Carré et 2 demi-cercles

Carré et deux demi-cercles

Une énigme résolue pas à pas. On verra que l'aborder n'est pas si simple que n'y laisse paraitre la figure.

Sommaire de cette page

>>> Carré et deux demi-cercles

>>> Identification des angles droits

>>> Triangles rectangles semblables

>>> Figure prolongée et valeur des aires des polygones

Débutants

Géométrie

Glossaire

Géométrie

Carré et deux demi-cercles – Problème		haut
Avec une figure simple, ce problème, demandant le calcul de l'aire d'un quadrilatère, n'est pas simple ! Surtout pas de calcul direct de l'aire, mais un raisonnement par comparaison des aires, notamment avec l'aide de triangles rectangles semblables.
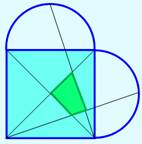
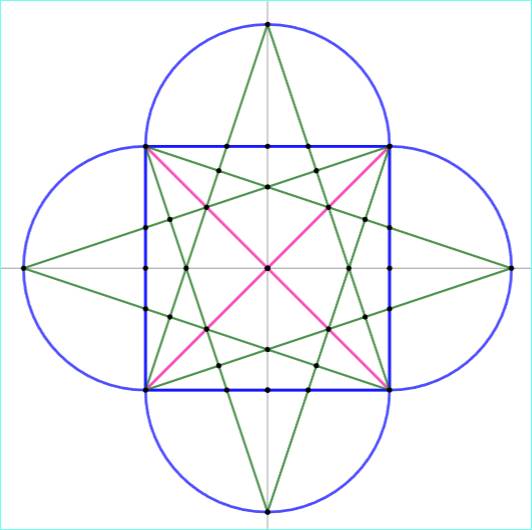
Construction Un carré et deux demi-cercles posés sur deux côtés adjacents du carré. On dessine (vert) les deux diagonales du carré et deux grandes obliques formées avec les sommets du carré et les points milieux des arcs de cercle. Ces quatre segments délimitent un quadrilatère. Montrer que l'aire de ce quadrilatère est égale au dixième de celle du carré. Piste La figure laisse deviner des angles droits (à confirmer), et donc la création de triangles rectangles et aussi de parallèles. 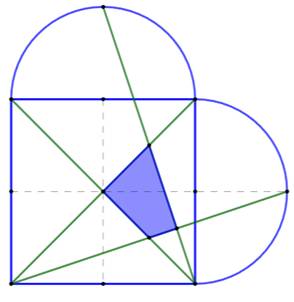*L'idée va consister à comparer les aires de triangles rectangles semblables.*	Figure initiale *Aire bleue = 1/10 Aire du carré*

Identification des angles droits

haut

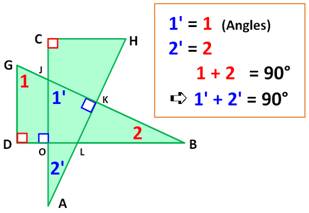
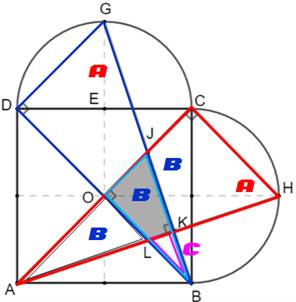
Angles droits

DE = EO = EG = rayon du cercle

Angle ODE = 45°; angle EDG = 45°
=> Angle ODG = 90°.
Idem pour OCH = 90°.

Même raisonnement pour l'angle OCH = 90°.

L'angle JOL est formé par les deux diagonales du carré; il est droit.

Voyons l'angle LKJ = AKG.

Les côtés des deux triangles rectangles ACH et BDG ont les mêmes dimensions: ils sont isométriques (superposables).

Ce sont deux triangles "orthogonaux" en O avec un angle formé par un côté et l'hypoténuse. L'angle réciproque en inversant côté et hypoténuse est également droit.

La figure illustre comment montrer que l'angle en K est droit.

Figure avec notations

Deux triangles rectangles orthogonaux isométriques

Triangles rectangles semblables

haut

Taille des triangles rectangles

Avec DG = 1 unité (sans perte de généralité)

Triangle BDG: avec DG = 1,
alors BD = 2 et BG = √5 (cf. BG² = 1² + 2²)

Compte tenu de leurs angles les triangles rectangles A, B et C sont semblables, et donc tous du type 1, 2, √5 (les proportions entres les longueurs des côtés)

Leurs aires sont dans les mêmes proportions, mais au carré.

Aire du quadrilatère (Q)

En termes d'aires:

Les triangles BJO et BJC avec un sommet commun et des bases (JO et FC) de même longueur ont la même aire B. On a aussi: 2B = 1/4 de l'aire du carré.

Figure montrant les aires des triangles rectangles: A, B et C

Figure prolongée et valeur des aires des polygones

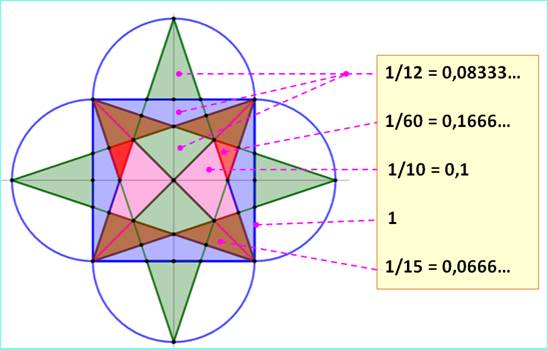
Somme des parties pour former le carré

Haut de page

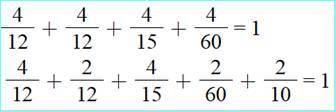
Retour	Défis en géométrie – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Carré dans le cercle Divers défis 02 Équation en x⁴ Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/Carr2Cer.htm