Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/10/2025 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Carré et cercle	Deux demi-cercles
	Coin du carré replié	Quatre cercles et carré	Demi-cercle et rectangle
	Quatre carrés	Carré et triangle équil.	Trapèze et triangle
	Carré oblique	Fourmi sur un pavé	Rectangles croisés
	Rectangle et deux cercles	Trois carrés plus un	Carré et 2 demi-cercles

Cercle et Carré Défi du cercle prisonnier du carré Cette énigme passe pour être très difficile. En fait, elle illustre le cas où, comme souvent, il faut bien réfléchir avant de lancer des calculs. D'abord bien comprendre la figure, et détecter ses propriétés sous-jacentes. Ensuite, imaginer une stratégie de calcul de l'aire basée sur additions et soustractions d'aires de formes connues. Bonne dégustation …
	Sommaire de cette page >>> Carré, cercle et rectangle >>> Pour s'entrainer >>> Le cercle prisonnier du carré	Débutants Géométrie Glossaire Géométrie

Carré, cercle et rectangle – Facile !		haut
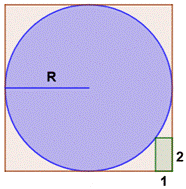
Construction Un cercle de rayon R inscrit dans un carré. Un rectangle 2 × 1 situé dans un coin du carré. Un de ses sommets est situé sur la circonférence du cercle. Quelle est la valeur du rayon R ? Piste Tracer le grand rectangle vert, sorte de complémentaire du petit rectangle vert. Ses dimensions: R – 1 et R – 2 Calculs Avec le théorème de Pythagore: R² = (R – 1)² + (R – 2)² R² = R² – 2R + 1 + R² – 4R + 4 R² – 6R + 5 = 0 Résolution de l'équation du deuxième degré: Solutions R = 5 La solution attendue (figure du milieu) R = 1 Une solution dégénérée (figure du bas)	Figure de l'énoncé Figure avec notations Solution dégénérée

Pour s'entrainer tout simplement		haut
Construction Un cercle de rayon unité et un point sur le cercle en guise de sommet d'un carré. La diagonale du carré porte un rayon du cercle. Quel est le côté x du carré de sorte que les aires A = B ? Piste Le rayon porté par la diagonale du carré fait un angle de 45° avec les côtés du carré. Il est possible de dessiner le carré bleu qui est inscrit dans le cercle. Le calcul des aires A et B sont alors simples à expliciter: A = Grand carré – B B = C + 2D Calculs	Figure initiale Figure avec notations

Le cercle prisonnier du carré		haut
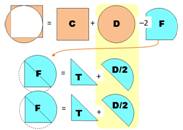
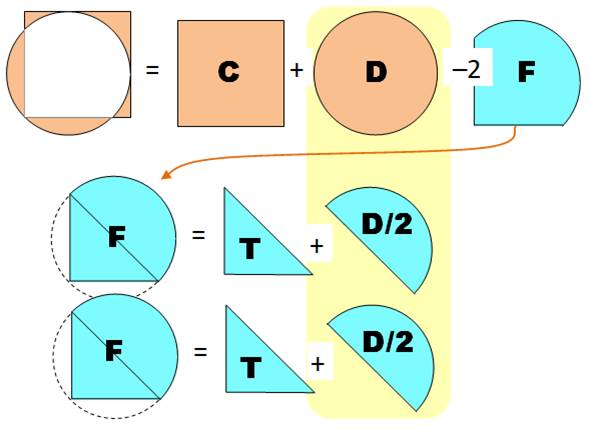
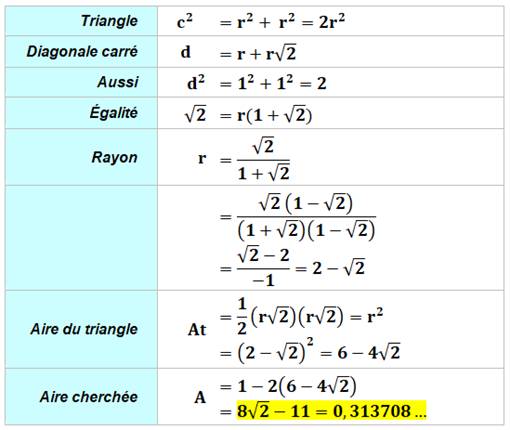
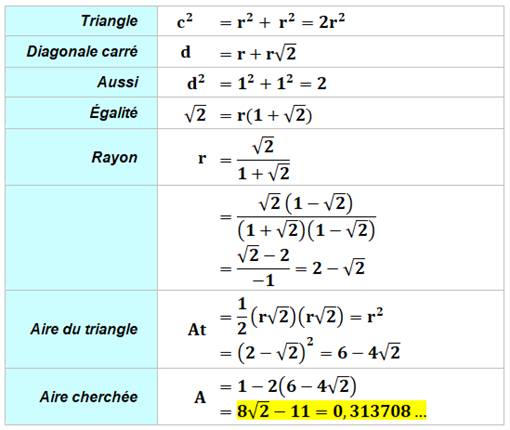
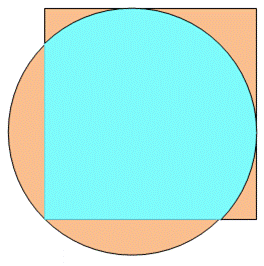
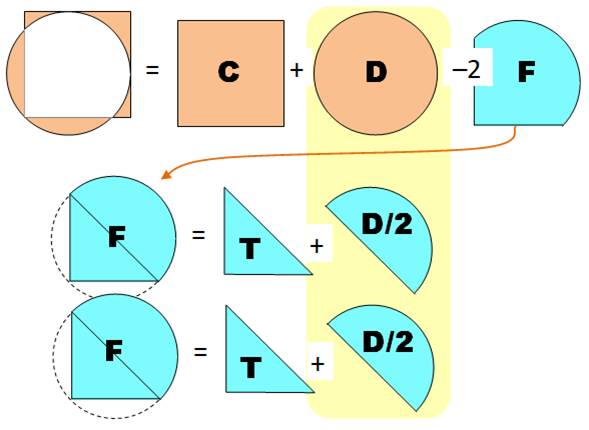
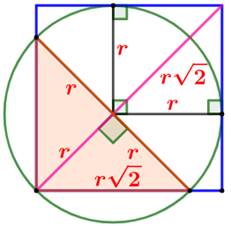
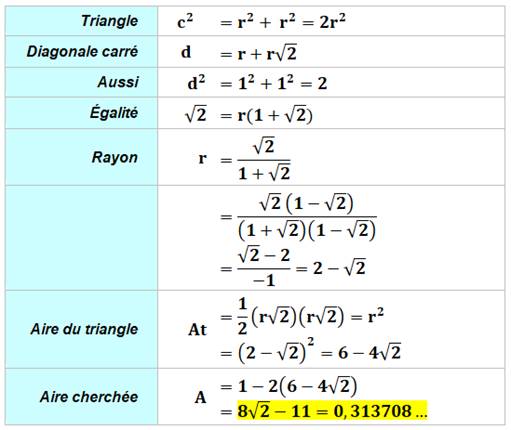
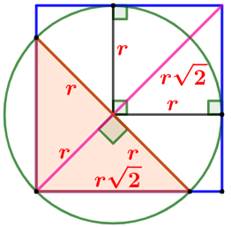
Construction Un carré de côté unité Un cercle passant par un des sommets du carré et tangent aux deux côtés opposés au sommet. Quelle est l'aire de la zone en marron ? Piste Le triangle coloré (figure en bas) est rectangle. Par symétrie, il est isocèle. L'angle droit intercepte un diamètre. Le centre du cercle est le milieu de l'hypoténuse du triangle (point rouge). Les rayons joignant les points de tangence sont en angle droit (c'est une propriété des tangentes à un cercle). Principe de calcul de l'aire On pourrait calculer cinq aires élémentaires de secteurs ou segments. Il existe une méthode plus simple: l'aire cherchée est celle du carré plus celle du disque auxquelles il faut retirer deux fois la zone centrale (bleue). Le dessin ci-dessous illustre le principe de calcul. Détails ci-dessous.

Arithmétique illustrée des aires

En jaune, l'aire relative au disque disparait dans cette opération.

L'aire cherchée vaut finalement celle du carré diminuée de deux fois celle du triangle.

Calculs

D'après: Very difficult for most students – Mind Your Decision – Presh Talwalkar

Haut de page

Retour	Défis en géométrie – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Carré dans le cercle Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CarreCer.htm