marche de l'ivrogne, évolution des espèces

INDEX Graphe Topologie Dénombrement Logique	GRAPHES
	Graphes – Introduction	Arbres – Introduction	Chemin le plus court
	Chemin eulérien	Cinq pays	Voyageur de commerce
	Graphe planaire	Trois maisons	Multiple et diviseurs
	Graphe de Delaunay	Petit monde	Nombres de Delannoy
	Ivrogne	Colonies de fourmis	Nœuds
	Chemin auto-évitant

Faites un double-clic pour un retour en haut de page

MARCHE de l'IVROGNE

ou marche aléatoire

Processus de progression discrète (pas à pas) dont l'étape suivante est lié à l'état présent et pas du tout à la mémoire du passé proche. Il revêt seulement un caractère de type probabilité (stochastique) dit markovien. Le mouvement brownien fait partie de la famille.

L'évolution des espèces procéderait-elle d'un tel processus?

Sommaire de cette page

>>> Marche de l'ivrogne

>>> Généralisation

>>> Évolution des espèces

>>> Types d'évolutions

Débutants

Dénombrement

Glossaire

Combinatoire

MARCHE de l'IVROGNE
Un ivrogne, sorti du bar, avance et recule au hasard entre le bar et le caniveau. Le trottoir fait 3 mètres et ses pas sont de 0,5 mètre. Quelle est la probabilité qu'il se retrouve dans le caniveau?	Probabilité moyenne que l'ivrogne tombe dans le caniveau: 1/8 = 0,125

La figure montre des exemples de trajet tirés au hasard (pile ou face, en fait ici utilisation de la fonction rand de Maple en donnant la valeur pile aux nombres pairs et face aux impairs. La diagonale rouge en bas est la trajectoire directe vers le caniveau. Nous ne sommes pas à l'abri d'une trajectoire longeant longuement le bar (rose en haut à gauche). Si l'ivrogne part du bar, il faudrait qu'il avance six fois de suite pour atterrir dans le caniveau. Ce qui est équivalent à tirer six faces de suite à pile ou face. La probabilité est 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 = 1/64 S'il part du milieu, s'il est à 1,5 m du caniveau, il faut qu'il avance trois fois de suite, soit une probabilité de 1/8 = 0,125.

Anglais: random walk

Généralisation

La particularité de l'exemple présenté est de montrer la probabilité avec " MUR ". L'ivrogne finira toujours dans le caniveau. Car du côté du bar, s'il est fermé, le pas en arrière sera toujours bloqué.

Un système en mouvement rectiligne, physiquement limité par un mur à une extrémité et soumis à une dynamique purement aléatoire, sans aucune direction privilégiée, voit inéluctablement sa position moyenne s'éloigner du mur, quelle que soit sa position de départ.

Évolution des espèces

La règle de Cope (1840-1897) dit que la taille des organismes tend à croître au cours de l'évolution. Cette règle est vraie à 70% environ, ce qui est déjà bien en biologie pour affirmer une tendance. On devrait trouver 50/50.

C'est un cas d'application d'une probabilité de croissance avec mur vers le bas. Il n'est pas paradoxal de voir les individus de tailles plus grandes apparaître avec le temps. Plus le temps passe, plus le haut du graphe présenté ci-dessus se remplit, et plus on trouve de tailles variées. Il faut leur laisser le temps de s'implanter. Rien à voir avec une tendance du type sélection naturelle des plus grands.

Thèse de Stephen Jay Gould (1941-2002) et d'autres

Les espèces améliorent leurs conditions grâce au forfait des inadaptés et non en construisant de manière délibérée un mode amélioré.

Type d'évolution
Évolution lamarckiste	Évolution mendélienne
ou transmission des caractères acquis. L'organisme détermine les traits adaptatifs favorables et les transmet par hérédité. L'évolution atteindrait rapidement son but, mais elle ne fonctionne pas comme ça: La girafe n'a pas un long cou pour atteindre les feuilles des arbres. Le forgeron a beau taper et développer de gros bras. Ses fils n'auront pas de gros biceps pour autant. Le changement culturel est sans doute lamarckien. On transmet le savoir à la descendance par l'éducation. Mais le phénomène est plus profond. La transmission lamarckienne du patrimoine culturel confère à l'histoire de la technologie un caractère cumulatif et direct, étranger à l'évolution naturelle des espèces.	Développement statistique avec mur, favorisant la diversité avec le temps. C'est l'évolution des espèces. Elle procède lentement et par voie indirecte. La girafe qui se trouve avoir un long cou a résisté car elle a pu se nourrir.
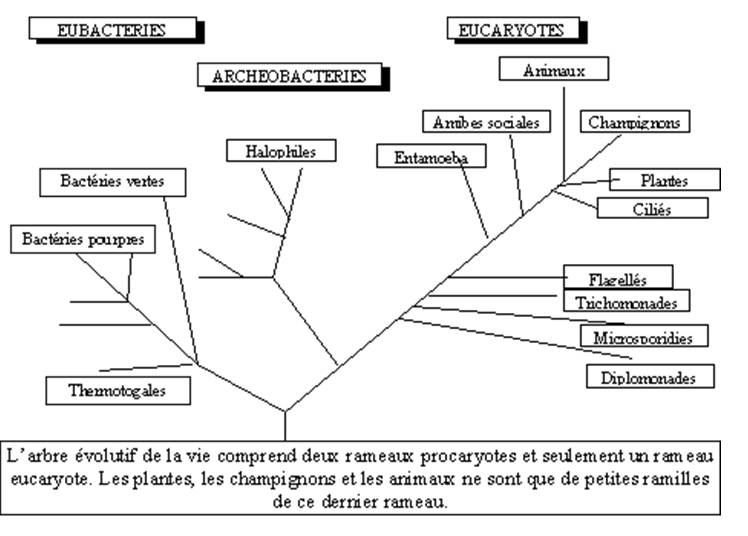
L'arbre évolutif de la vie

L'excellence se manifeste en des milliers d'endroits et nous devons lutter en chacun de ces endroits pour la préserver.

Il faut éviter la propagation de la médiocrité uniforme.

Suite	Chemin le plus court Graphe – Index
Voir	Code Gray Croissance logistique Diagramme de Venn Dominos et graphe Échiquier et graphe Énigmes et paradoxes Intelligence artificielle Jeux – Index Logique formelle Médaille Fields: Wendelin Werner Nombres de Delannoy Raisonnement Topologie – Glossaire Tour de Brahmâ
DicoNombre	Nombre 0,125
Cette page	http://diconombre.fr/LogForm/Ivrogne.htm