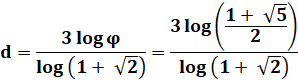|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITE DE FIBONACCI et Nombre d'or Propriétés Fractales Si la suite de Fibonacci est de nature récursive (chaque valeur est
construite à partir des valeurs précédentes), elle n'est pas de nature fractale; elle n'est pas auto-similaire (pas
de répétitions à l'infini de motifs similaires). Pourtant, l'imagination des amoureux de cette suite a
conduit à dénicher des recoins fractals … Il existe notamment une figure
fractale formée à partir du mot
binaire Fibonacci. Note: le chou Romanesco fait penser à une
structure fractale impliquant la suite de Fibonacci. |
|
|
||
|
Mot Fibonacci se réfère à une
suite de 0 et de 1 qui pourrait tout aussi bien être une suite de deux
lettes. L'idée de
la construction d'une courbe fractale consiste à interpréter ces chiffres
binaires comme des instructions de dessin. |
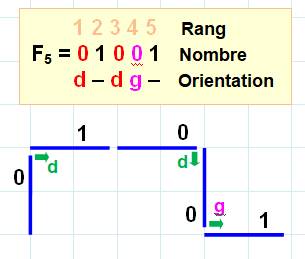
MF4 = 010 MF5 = 01001 MF5 = 01001010 Trois nombres successifs, et principe de la
construction de M5. |
|
|
Instructions Pour
chaque chiffre: dessiner un trait unitaire. Si le
chiffre est "0" en fin de trait: tourner d'un quart de tour: - à
droite si le rang du chiffre est impair; - à
gauche, si le rang est pair (odd-even draw rule). Exemple
avec F5 Un trait vertical (ou horizontal).
Le zéro en position impair impose un quart de tour à droite. Avec le 1, dessin d'un trait
simple; on conserve la direction. Avec le 0 de rang impair,
dessin d'un trait et quart de tour vers la droite. Avec le 0 suivant de rang
pair, le trait est suivi d'un quart de tour vers la gauche. Et avec le 1 final, dessin
d'un trait simple. |
Exemple de construction
Chaque nombre Fibonacci peut être dessiné
indépendamment des autres. |
|
|
La
droite a une dimension 1 et la surface, une dimension 2. Cette
ligne du mot Fibonacci qui court sur le plan sans jamais se recouper à une
dimension intermédiaire: 1,637938208 …
Avec phi, le nombre d'or:
|
Construction des
courbes jusqu'à M14
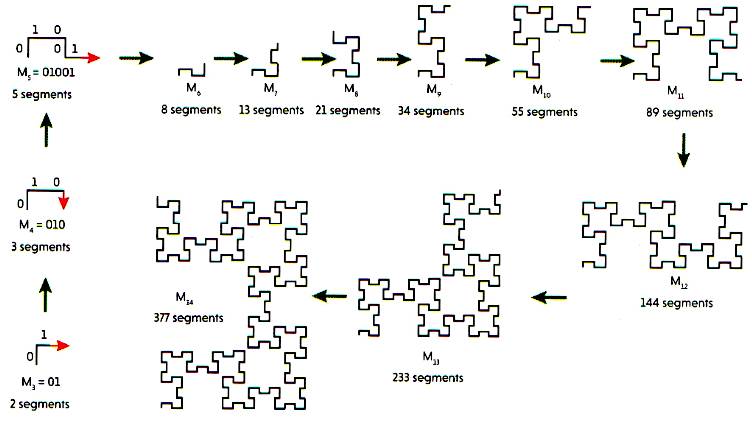
Source image:
N°478 Pour la Science et The Fibonacci Word fractal
Voir Courbe jusqu'à F23
|
|
||
|
Dessin à partir du mot Fibonacci
Note:
exercice de programmation amusant, mais la valeur du mot Fibonacci dépasse
vite la capacité du logiciel. Il est très difficile d'imaginer aller plus
loin que le septième mot. |
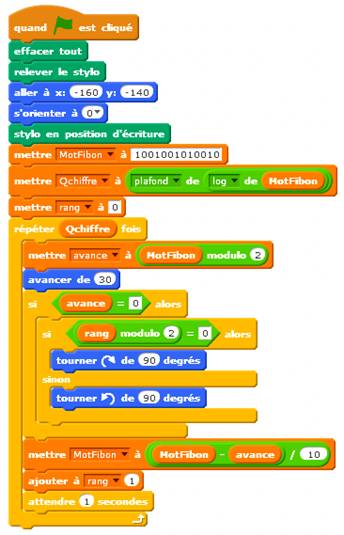
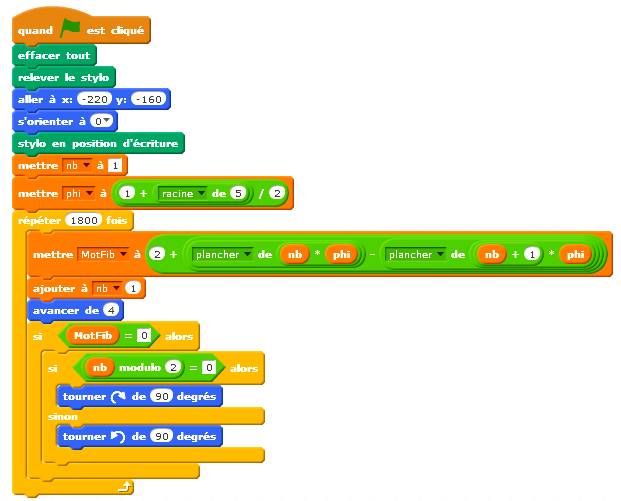
Commentaires Initialisation en effaçant et mettant le stylo en
position de départ. Préparation du mot de Fibonacci (ici MF7)
entré à la main. Calcul de "Qchiffre", la quantité de chiffres (attention au zéros au
départ qui sont ignorés par ce type de calcul). La variable "rang" indiquera si le
chiffre est au rang pair ou impair. Lancement de la boucle pour "Qchiffre"
répétitions. La variable "avance" est en fait égale
au reste de la division par 2 qui est soit 0 ou 1 et qui va guider la
progression du dessin. Si cette variable "avance" est à 0
tourner à droite ou à gauche selon la parité donnée par la variable
"rang". Supprimer un chiffre au MotFibon et augmenter le
rang d'une unité. L'attente est facultative. Elle permet de voir
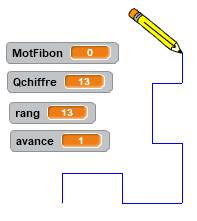
évoluer les compteurs Résultat de l'exécution du programme
|
|
Voir Programmation
avec Scratch
|
Dessin avec calcul des chiffres un à un Cette méthode évite la mémorisation des mots Fibonacci qui deviennent
vite très longs. On reprend la formule
de calcul du énième chiffre du mot Fibonacci
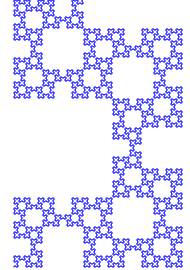
Résultat de l'exécution du programme avec 1700
pas de 4 et 7000 pas de 1
|
Voir Programmation
de fractales avec Scratch
Résultat
de l'exécution du programme avec 28 657 = F23
pas de 0,5

|
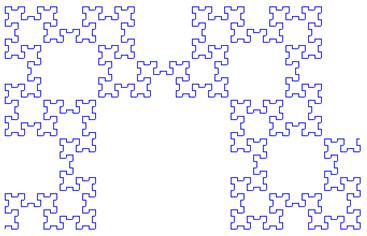
Les
couronnes autour des carrés de taille de plus en plus petite montrent la
nature auto-similaire (fractale) de cette courbe Pour
encore mieux visualiser la nature fractale de cette courbe voir les images
sur le site The Fibonacci Word fractal. Vous pouvez vous régaler à construire cette
courbe avec Scratch. Logiciel gratuit et avec emploi ultrasimple et immédiat. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Sites |
|
|
Cette page |
![]()