NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/01/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Itérations
Débutants Général	Suite de Fibonacci			Glossaire Général
INDEX Fibonacci	Suite de Fibonacci	Parcours	Escalier
	Suite de Lucas	Lapins	Nature
		Blocs 01
		Sommaire de cette page >>> Approche >>> Fibonacci >>> Démonstration

Blocs de "1" ou "0"

dans un nombre binaire

En écrivant tous les nombres binaires de longueur n, nous serions étonnés de retrouver la suite de Fibonacci, nichée là. Il suffit de compter la quantité de nombres en excluant ceux qui comportent des blocs de trois "1" ou de trois "0".

Approche
Un nombre binaire de 3 bits. Parmi toutes les possibilités, combien comprendrons un bloc de trois "1" ou un bloc de trois "0"? Ou, combien sont exempts de ces blocs? Notons Qn la quantité sans blocs de trois pour un nombre de n bits. Ici Q3 = 6.	Sur 2^3 = 8 cas, 6 sont sans blocs de trois "0" ou trois "1".
Pour les nombres de 1 ou 2 bits, il n'y a pas de blocs de trois.	Q1 = 2 = 2^1 Q2 = 4 = 2^2 Q3 = 6 = 2^3 – 2 x 1
Pour un nombre binaire de longueur 4, il y a 2^4 = 16 cas dont 2 x 3 sont des blocs de "1" ou de "0". Non la suite n'est pas faite des nombres pairs successifs!	Q4 = 10 = 2^4 – 2 x 3

Fibonacci
La séquence trouvée ci-dessus est en fait la suite de Fibonacci, doublée.	Fn = { 1, 1, 2, 3, 5 … } Qn = { 2, 4, 6, 10 …}
Le cas n = 5, nous laisse penser que nous sommes sur la bonne piste. Mais voyez comme le dénombrement n'est pas évident sans y regarder de près.	Q5 = 16 = 2^5 – 2 x 8 Q5 = 2 x F6

Démonstration
Nous allons retrouver une suite semblable à celle que nous connaissons bien: les commentaires numériques. Ayant interdit les blocs de trois, ce nouveau nombre ne contient que des 1 et des 2 et pas de 3.	Nombre binaire de 8 bits (n = 8) 10110010 En notant la quantité de chiffre, cette suite devient: 112211
L'idée consiste à trouver une formule de récurrence.	Qn = Qn – 1 + Qn – 2
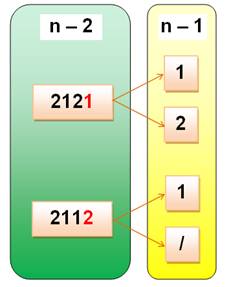
Partant d'un nombre ne n-1 bits, deux cas de figure se présentent pour passer au suivant à n bits.	La suite en "12" se termine par 1 ou par 2.
Si avec n – 1 bits, la suite "12" se termine par 1 (un chiffre unique, le "1" ou le "0"), le bit suivant peut être 0 ou 1n voire 00 ou 11, selon le bit terminal du nombre n-1. Par contre si la suite "12" se termine par 2, nous savons que nous avons déjà deux chiffres identiques; il ne reste qu'une seule possibilité: placer un seul "1" ou un seul "0" pour former le nombre à n bits. Bilan: dans tous les cas, soit Qn – 1, nous aurons les possibilités de placer un chiffre en plus: Qn = Qn – 1 + "les cas avec 2 en n"	Dans tous les cas, on retrouve un "1" en passant en n. Le "2" n'est possible que si le précédent est "1".
Le seul cas où un "2" est engendré en n, c'est lorsqu'il y a un "1" en n – 1. Avec le même raisonnement que ci-dessus, le nombre de cas de cette espèce est égal à Qn – 2. Qn = Qn – 1 + Qn – 2 On prendre les valeurs Q1 = 2 et Q2 = 4 pour amorcer la récurrence. On note qu'il s'agit de la suite de Fibonacci doublée; ou de la suite simple pour les "1" et idem pour les "0".	Le niveau n-2 engendre des "1" à tous les coups au niveau n - 1, lesquels engendrent des "2" à l'étape suivante n.

Suite	Escalier et Fibonacci Parcours du taxi Voir menu en haut de page
Voir	Calcul mental – Index Chaîne d'Or Croissance logistique Géométrie – Index Graphes et chemins optimums Jeux – Index Nombre d'or Voyageur de commerce
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Fibo01.htm