![]()
|
|
Ce site est
désormais accessible en http://diconombre.fr/index.html et pour cette page voir le lien en fin de page For this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||
![]()
|
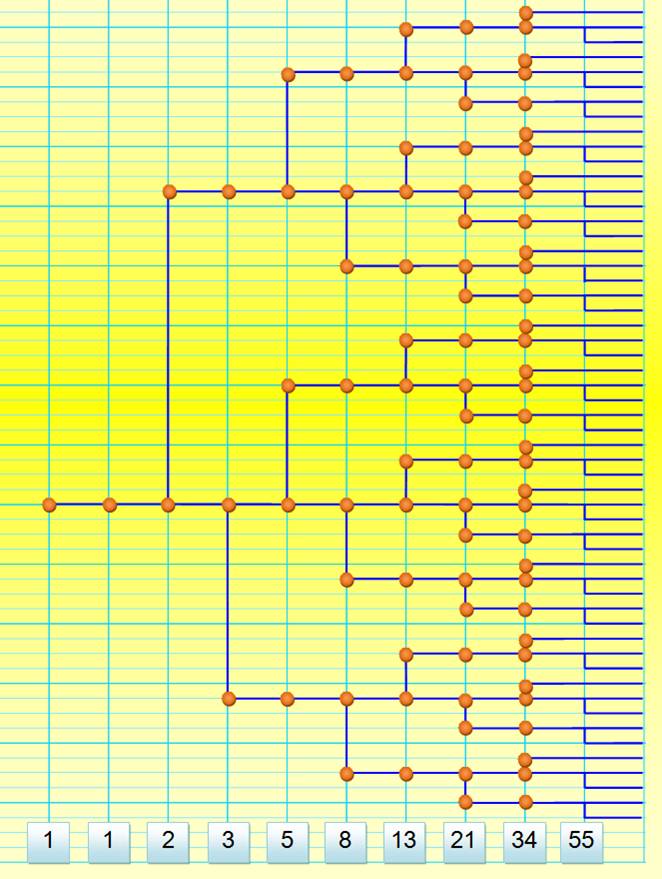
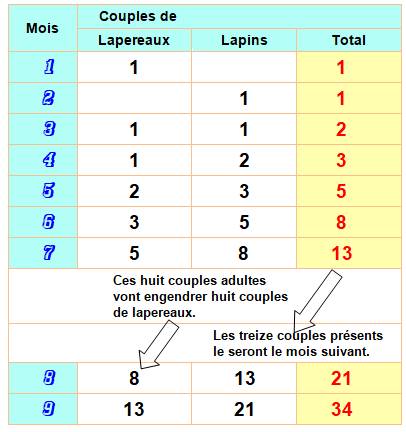
Suite de Fibonacci LAPINS Leonardo
Pisano Fibonacci (v. 1175 – v. 1250) est le plus connu
des mathématiciens du Moyen Âge.
Il est surtout connu par la suite de nombres qui porte son nom*. Elle aurait été découverte en
comptabilisant les lapins suite à leur reproduction. Fibonacci met au point
la formule qui permet de déduire la quantité de lapins de la saison suivante
à partir des quantités des saisons précédentes. Cette formule devient la
première formule avec récursivité connue de l'histoire. Ce fut une contribution
majeure à la partie des maths nommée combinatoire. * J'avais écrit suite de nombres éponyme et Jean-Claude I. me corrige avec
raison, car éponyme veut dire: qui porte son nom. On pourrait écrire: Fibonacci est le
mathématicien éponyme d’une suite de
nombres qui a fait de lui l'un des savants les plus connus du Moyen Âge. Voir Éponyme dans le DicoCulture |
Anglais: The problem of rabbit's reproduction
|
|
|
|
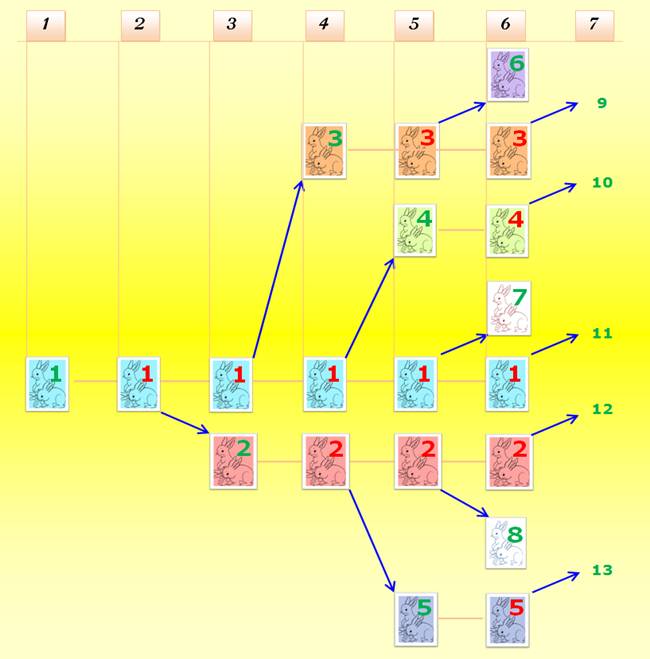
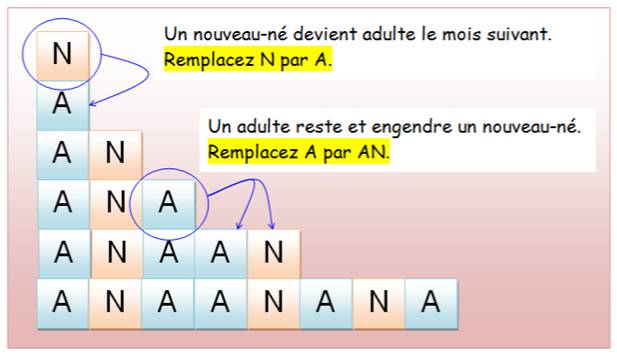
Les naissances des lapins
selon Fibonacci
Illustration
Explications
Qtén+1 = Qtén + Qté de ceux qui peuvent procréer Or, ceux qui peuvent procréer étaient présents l'année précédente. Qtén+1 = Qtén
+ Qtén-1 |
|
|
|
|
|
|
|
|
|
Merci à Vincent Thominet pour sa contribution
|
|
|
|
Qn+1 = Qn + Qn–1
|
|
Bilan
|
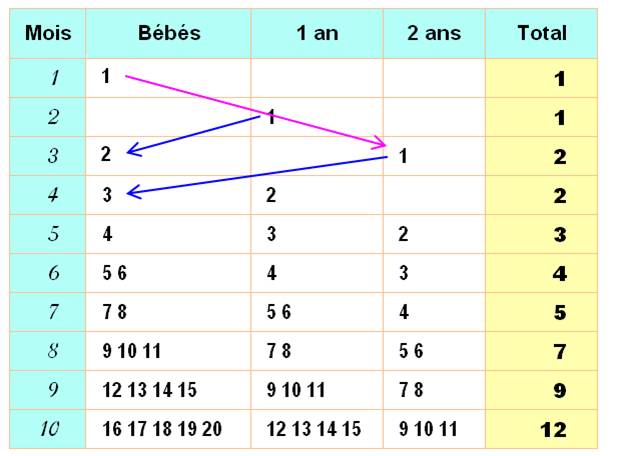
Le mode de
reproduction des lapins n'est sans doute pas exactement conforme à cette loi.
Notamment, une portée n'est que rarement limitée à un couple male-femelle. De
plus, ils ne vivent pas indéfiniment … Voir Croissance
logistique qui tient compte du manque de nourriture. |
|
|
|
|
Qn+1 = Qn–1 + Qn–2 C'est la suite de Padovan. |
|
|
|
|
|
|
|
Voir Azaazaza
|
|
||||||
|
0 1 10 101 10110 (101 vient du dessus et 10 de la ligne d'avant) 10110101 1011010110110 101101011011010110101 10110101101101011010110110101101
C'est
la suite OEIS A003849 – The infinite
Fibonacci word (start
with 0, apply 0->01, 1->0, take limit). Illustration
originale
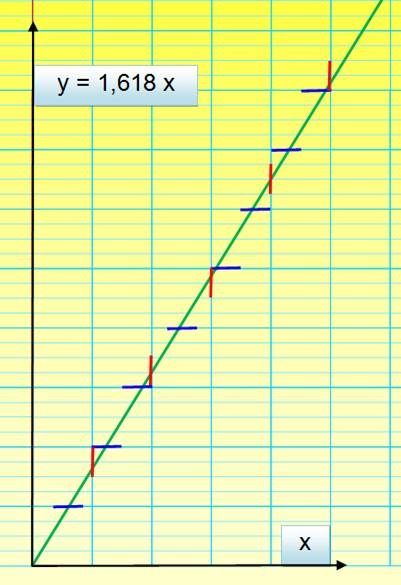
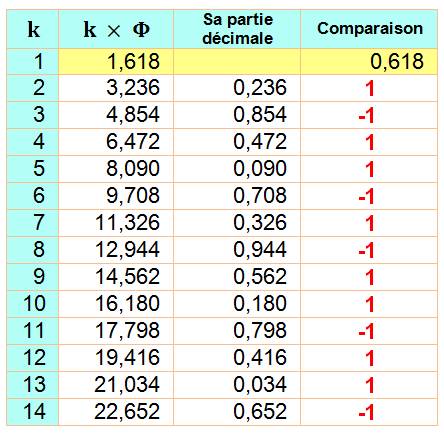
Constante
du lapin (rabbit constant)
Autres
façons de créer la suite binaire dorée
Pour les cinquante
premiers multiples
C'est
la suite OEIS A005614 - The binary
complement of the infinite
Fibonacci word A003849 (décrite ci-dessus).
|
||||||
|
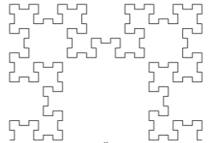
Fractale
Notes: Plus d'information sur le site indiqué.
Il existe aussi une figure fractale dite lapin de Douady qui n'a rien à voir
avec celle-ci. |
|
|||||
Voir Fibonacci et
fractales / Spectre numérique
d'un nombre réel
|
|
||
|
|
Commentaires La programmation est assez élémentaire. Les premières valeurs sont placées en a et b. Une
troisième variable c est mise en jeu pour mémoriser temporairement le total. La boucle for … do … od fait tourner une boucle de
calcul dix fois. Le calcul du total a + b est placé en c et les
valeurs de a et b sont mises à jour. L'impression donne le rang (deux de plus que le
pointeur i) et la valeur numérique du total c. |
|
Voir
Programmation
Fibonacci en Scratch / Programmation
des k-bonacci / Programmation – Index
![]()
|
Voir |
|
|
Site |
|
|
Cette page |
![]()