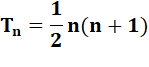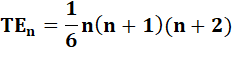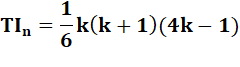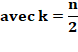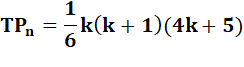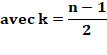Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 19/01/2025 M'écrire Brèves de Maths

INDEX Sommes de nombres Somme-Produit Ch Identités Calcul Types de nombres Jeux et énigmes	Sommes de nombres
	Approche	Index et formules	Somme des entiers
	Sommes de chiffres	Somme des inverses	Somme alternée
	Sommes de carrés	Somme des triangulaires	Démonstrations

Faites un double-clic pour un retour en haut de page

Sommes des nombres triangulaires Les sommes des nombres triangulaires successifs forment la suite des nombres tétraédriques. Comment calculer la somme des nombre triangulaires d'indice pair ou d'indice impair ? Application au calcul de la quantité de triangles équilatéraux dans le triangle équilatéral.
	Sommaire de cette page >>> Somme des nombres triangulaires >>> Démo – Tous >>> Démo – indices MIPAIRS >>> Démo – indices PAIRS	Débutants Nombres Glossaire Nombres

Somme des nombres triangulaires		haut
Nombres triangulaires Le nombre triangulaire Tn est la somme de tous les nombres entiers jusqu'à n. Les premiers nombres triangulaires: 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, …	Formule des nombres triangulaires Voir Comment établir cette formule
Nombres tétraédriques: somme des triangulaires Le nombre tétraédrique TEn est la somme des nombres triangulaires successifs jusqu'à l'ordre n. Les premiers nombres tétraédriques: 0, 1, 4, 10, 20, 35, 56, 84, 120, 165, …	Formule des nombres tétraédriques
Somme des triangulaires d'indice IMPAIR Le nombre tétraédrique TIk est la somme de k nombres triangulaires d'indice impairs. Alors n = 2k. Exemple avec n = 6 et k = 3 TP3 = 1 + 6 + 15 = 22 = 3 × 4 × 11 / 2 = 22	Formule des triangulaires pairs
Somme des triangulaires d'indice PAIR Le nombre tétraédrique TPnk est la somme de k nombres triangulaires d'indice pairs. Alors n = 2k + 1. Exemple avec n = 5 et k = 2 TP2 = 0 + 3 + 10 = 13 = 2 × 3 × 13 / 2 = 13	Formule des triangulaires pairs

Démo – Tous	haut
Démonstration par induction

Démo – indices MIPAIRS	haut
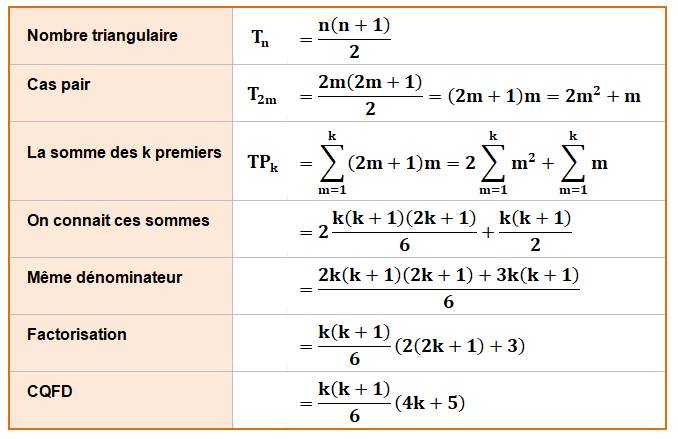
Démonstration par somme composée

Voir Somme des nombres carrés, Somme des entiers

Démo – indices PAIRS	haut
Démonstration par somme composée

Haut de page (ou double-clic)

Retour	Somme de nombres – Index
Suite	Quantité de triangles équilatéraux dans le triangle équilatéral Nombres triangulaires – Introduction et développements Nombres tétraédriques Relation de Fermat Nombres proniques Nombres parfaits Racine triangulaire et tour de Hanoï
Voir	Nombres figurés
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomTrian.htm