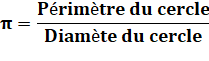|
Édition du: 22/12/2021 |
|
INDEX |
Types de Nombres |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Pourquoi Pi n'est pas un nombre
entier ? Dis-moi,
tonton: une boule de billard toute
lisse a un volume fini, par exemple 100 cm3. Donc le nombre
Pi doit être fini aussi, autrement c’est impossible ! Comment tu
expliques cela ?
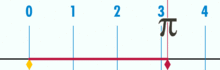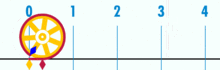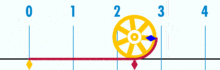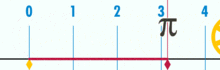
L'illustration
montre que Pi est le périmètre d'un cercle de diamètre unité. Source animation:
Wikipédia |
||
|
|
Sommaire de cette page >>> En bref >>> Cas du carré et de sa diagonale >>> Cas de la sphère et de son rayon >>> Maths et Physique |
Débutants Glossaire |
|
La droite des nombres Les valeurs
(longueurs, aires, volumes, …) peuvent être représentées par des points sur une
droite, et il y en a une infinité. Certaines valeurs sont des nombres entiers ou des
fractions (nombres rationnels) et beaucoup
("très beaucoup") d'autres sont des nombres avec des décimales qui
n'en finissent pas (nombres irrationnels).
Notez que rationnel vient
de ratio, un autre mot pour fraction. |
La boule de billard Le volume et le diamètre de la boule de billard
sont deux valeurs représentées par des points, quelque part sur cette droite.
En règle générale, ces deux valeurs sont
quelconques, avec une très grande probabilité d'être irrationnelles. Mais si, par hasard, l'une est rationnelle
(un entier ou une fraction), il est très probable que l'autre soit dans le
lot des irrationnelles.
C'est le cas pour le cercle ou la sphère. |
|
|
Exemple de représentation de deux
valeurs: un nombre entier (3) et un nombre quelconque (1,44321…)
|
||
|
Aventure à l'école de Pythagore Pythagore et
ses collègues (son école) ne juraient que par les nombres entiers. Pourtant, ils sont tombés sur un os en voulant
exprimer la longueur de la diagonale d'un carré de côté unité. Elle vaut en
effet: racine
de 2 =
1,41421… Consigne avait été donnée de ne pas en parler. Pourtant
l'un des membres de l'école mourait d'envie de divulguer le fait qu'il
existe des nombres spéciaux, que l'on ne peut pas exprimer par une fraction
(nombres irrationnels – "pas de ratio"). On l'a emmené au large sur
un bateau pour y être noyé ! |
Cas du carré Le carré
de côté unité a une diagonale qui mesure 1,4142… un nombre irrationnel. Ou, si l'on se donne une diagonale égale à 1, le
côté sera mesuré par un nombre irrationnel:
0,7071… Conséquence de cette découverte: il existe des
objets mathématiques comme le simple carré pour lesquels se donner un nombre
entier pour une mesure engendre des nombres irrationnels pour la mesure de
certaines autres parties. |
|
|
Côté
du carré et sa diagonale: lorsqu'une mesure est un entier, l'autre est irrationnelle
Voir Théorème de Pythagore (a² + b² =
c²) |
||
|
Cas du cercle ou de la sphère Eh, oui, on a fait la même découverte pour le cercle
et la sphère,
mais en pire! La mesure n'est plus la racine carrée d'un
nombre, mais un nombre spécifique à ces formes courbes, la constante Pi. Là aussi, se donner une mesure entière pour une
dimension engendre des dimensions irrationnelles pour d'autres. |
Constante Pi Cette constante est un nombre irrationnel, ses
décimales se déroulent sans fin. Pour le calculer, on a beau dessiner des cercles
de plus en plus grands pour augmenter la précision, on trouve toujours des
chiffres nouveaux. Pourtant, il y a une bonne nouvelle, c'est le
même Pi qui sert pour toutes les formes rondes. |
|
|
Définition
de Pi
|
Volume
de la sphère
|
|
Voir Évaluation
de l'aire du disque
|
Maths et infini. Nous venons de tenir un raisonnement purement
mathématique, c'est-à-dire dans un monde idéal où le point
est infiniment petit. Où, la quantité de points sur une droite est infinie.
Même si vous en "chopper" un, il en existe encore d'autres plus
petit. Parmi eux, il y en a qui, avec notre représentation
décimale, sont mis en vedette: ceux qui tombent justes qui correspondent
à un nombre entier dans notre système
arbitraire de nombres. Un de leurs voisins est jaloux car pour lui, il
faut une fraction (comme 1/2 = 0,5 ou même
1/3 = 0,333…). Une
multitude d'autres devraient se révolter car ils sont réduits à des racines de nombres (souvent avec une suite
infinies de décimales). Encore pire, beaucoup d'autres se cachent ! Il
n'y a rien pour les représenter, pourtant ils sont de loin les plus nombreux. Ah, si quelques uns ont réussi à se distinguer.
Le plus connu est Pi. Un autre est la constante "e", utilisée
lorsqu'on parle de croissance exponentielle. Voir Types
de nombres En résumé En maths on distingue les nombres rationnels et les nombres irrationnels. On sait démontrer que racine de 2
est irrationnel et que Pi
est un aussi un nombre irrationnel. |
En physique Dans le monde réel et avec nos instruments de
mesure, le volume de la boule est 100,00 cm3. Le diamètre mesure 5,76 cm. Si on calcule avec la formule du volume:
On retrouve le volume mesuré, à un
"poil" près. En utilisant des instruments plus précis, on peut
calculer la valeur de Pi. On trouvera par exemple: 3,1416. Encore plus précis, on va trouver de plus en plus
de décimales pour Pi, sans que l'on puisse atteindre le bout. Il y a une
infinité de décimales. En classe C'est une convention (un cas d'école, des valeurs
choisies pour un exercice) que de prendre un nombre entier pour un volume ou
autres. Dans le cas général, on aura plutôt des nombres
quelconques. En résumé Dans la réalité (en métrologie), on mesure avec
un instrument et cela, jusqu'à une certaine précision. Les lois de la physique (depuis Planck) montrent
qu'il y a une limite physique à la mesure (que l'on est loin d'atteindre
aujourd'hui car très inférieure à la taille d'un atome.) |
|
Merci à D. Dupont pour l'idée de cette page
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |