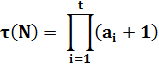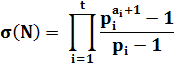NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/05/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Diviseurs
Débutants Division	Types de nombres selon leurs diviseurs			Glossaire Général
INDEX Décomposition Diviseurs	Présentation	Parfait	Presque parfait	Amiables
	de 1 à 100	Démonstration	Unit. Parfait	Sublimes
	Départ puis démonstration		Sommaire de cette page >>> Définition >>> Liste >>> Propriétés >>> Relations chez les diviseurs >>> Relations chez les sublimes >>> Démonstration

NOMBRES SUBLIMES

On considère les diviseurs d'un nombre;

On effectue leur somme;

On compte le nombre de diviseurs;

Ces deux derniers nombres sont parfaits.

Anglais: Sublime numbers

Définition
Nombre sublime: La quantité de diviseurs et la somme des diviseurs sont deux nombres parfaits. Exemple: 12 est un nombre sublime. Diviseurs 1, 2, 3, 4, 6 et 12 Quantité 6 Nombre parfait Somme 28 Nombre parfait

LISTE

En 2012, deux seuls nombres sublimes sont connus, S₁ = 12 et S₂ un nombre à 76 chiffres:

S1	= (2^2) (2^2– 1) avec 3 – 1 = 2 M3 étant un Mersenne premier.
S2	= (2^126) (2^61– 1) (2^31– 1) (2^19– 1) (2^7– 1) (2^5– 1) (2^3– 1) avec 127 – 1 = 126 = 61 + 31 + 19 + 7 + 5 + 3 M127 étant un Mersenne premier. = 0,608… 10^76 = 608655 5670238378 9896703717 3424316962 2657830773 3518859705 2832486051 2791691264

Il n'en existe probablement pas d'autres; ou, du moins, ils seraient extraordinairement grands; au delà des possibilités de test des moyens actuels.

S₂ est bien sublime (Vérification avec Maple)

PROPRIÉTÉS

Les nombres sublimes sont en relation avec les nombres de Mersenne premiers (M). Ils sont de la forme: S = (2^M – 1) (2^M1– 1) (2^M2– 1) … (2^5– 1) (2^3– 1) Avec M et les Mi, indices de nombres de Mersenne premiers et distincts tels que le plus grand moins 1 est la somme des plus petits: M – 1 = M1 + M2 + …+ 5 + 3 Le nombre 126 est la somme de six nombres de Mersenne premiers et distincts: 126 = 61 + 31 + 19 + 7 + 5 + 3. Il est la base du second nombre sublime.

** Démonstration (niveau supérieur)

(Énumération de pré-requis suivi de la démonstration)

Relations chez les diviseurs
Tout nombre est de la forme:
Quantité de diviseurs:
Somme des diviseurs:
Un diviseur de N en particulier contribue à la somme de cette manière (chacun des termes indiqués est un diviseur de N).
Si un facteur premier p est différent de 2, il est impair et la contribution à la somme devient:	Cette somme est paire pour a impair; comme, par exemple: 1 + p + p² qui est impaire pour a = 2.
Si la puissance a du facteur premier est impaire avec a = 2b+1. Avec l'exemple de p^5 pour comprendre le principe de la factorisation.

Relations chez les sublimes
Un nombre parfait est de la forme:	avec premier (Mersenne). Produit d'un impair par un pair
Somme de diviseurs d'un produit de nombres de Mersenne premiers.
Facteurs: ils sont de parités opposées.	2^s – 1 est une puissance de 2, donc paire. 2^s – 1 est impair pour deux raisons: c'est une puissance de 2 moins 1, c'est un nombre premier.
Un nombre sublime sera tel que: Les facteurs en jaune sont premiers.

Démonstration
Première étape	On isole les facteurs de N en puissance de deux.
N est divisible par 2^k	N = 2^k N'
Alors (voir ce lien):	est divisible par , un nombre impair.
Comparons (en jaune, premier)	= impair x pair = impair x pair
Déduction	2^k+1 – 1 est premier impair, un nombre de Mersenne et D = 2^s – 1
Deuxième étape	Quels sont les autres facteurs de N
Ce qui veut dire que tous les autres facteurs de N doivent contribuer à former	un facteur de 2^s – 1 pour , facteur qui est donc un nombre pair.
Seul un produit de nombres de Mersenne premiers et distincts est capable de donner une somme de diviseurs en puissance de 2.
Retour vers le nombre N	N = 2^k . Mp . Mq . Mr…. (N) = (2^k + 1 – 1) 2^p + q + r + …
Exemple Les Mersennes étant premiers, les contributions à la somme des diviseurs sont bien séparées et se multiplient.	N = 2^5 x 3 x 5 x 7 (2^5) = 63 = 2^5+1 – 1 (3x5x7) = 1024 (N) = 63 x 1024 = 64 512
Or sigma de n est parfait, ce qui impose la relation sur les indices	k + 1 – 1 = k = p + q + r +…
Ce qui veut dire qu'il faut trouver des Mersennes premiers distincts	tels que leur somme soit égale à k + 1.
Passons à la quantité de diviseurs	qui est aussi un nombre parfait
N est en puissance de 2 et en produit de Mersennes premiers
En sommant tous ces nombres de diviseurs	= (k + 1) x 2 x 2 x 2 x … = k + 1 + 2^h h étant la quantité de Mersenne dans N
Or cette quantité de diviseurs est parfaite
En comparant	k + 1 = 2^s – 1 , un Mersenne premier 2^h = 2^s – 1,
Ce qui donne deux conditions en plus:	k + 1 est un nombre de Mersenne premier. la quantité de Mersenne dans n est imposée.

Exemples avec ces conditions

N = 2^k . Mp . Mq . Mr…. k = p + q + r +… Mk + 1 Mersenne premier

Premier exemple	M2+1 = 2^3 – 1 = 7 Mersenne premier k = 2 p = 2 avec M2 = 2^2 – 1 = 3 Mersenne premier
Alors, expression du premier nombre sublime:	(N) = 28 (N) = 6

Pour les exposants suivants	3, 7, 15, 31, 63, 127
Pas de chance	6 n'est pas somme de 2 Mersenne premiers; 30 n'est pas somme de 4 Mersenne premiers;

Le suivant fait l'affaire comme somme de 6 Mersenne premiers.	126 = 61 + 31 + 19 + 7 + 5 + 3
D'où un nouveau nombre sublime:	N = 2^126 (2^61 – 1) (2^31 – 1) (2^19 – 1) (2^7 – 1) (2^5 – 1) (2^3 – 1)
Ce nombre vaut:	608655 5670238378 9896703717 3424316962 2657830773 3518859705 2832486051 2791691264
Somme des diviseurs; nombre parfait.	1447401 1154664524 4279463731 2608598848 1573677491 4748358890 6635434913 1199152128
Quantité de diviseurs; nombre parfait.	8128

Suite	Nombres parfaits Voir haut de page
Voir	Nombres économes, équidistants et prodigues Théorie des nombres – Index Calcul mental – Index Géométrie – Index
Site	Sublime numbers (qui a inspiré la démonstration exposée ci-dessus) OEIS A081357 – Sublime numbers Sublime number – Wolfram Mathworld
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Sublime.htm