NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Théorie mathématique			Glossaire Carrés magiques
INDEX Carrés magiques Calculs Jeux	Construction	Méthode d'Euler	Méthode diagonale	Symétrie
	Latin	Gréco-latin	Échelle alternée	Parallélogramme
	Tapis (prog)	Carré des entiers
		Sommaire de cette page >>> Méthode générale dite des symétries pour les carrés associatifs d'ordre impairs >>> Principe 1 – Somme >>> Principe 2 – Travailler les coins >>> Principe 3 – Configuration équilibrée >>> Principe 4 – Dernier choix et finalisation >>> Exemple 5x5 avec une autre symétrie >>> Exemple 7x7

Mathématiques des Carrés Magiques

La méthode des symétries

Méthode générale de construction des

carrés magiques associatifs d'ordre impair

basée sur la symétrie d'un carré associatif.

Méthode générale dite des symétries pour les carrés associatifs d'ordre impairs
À la recherche d'une méthode universelle pour les carrés magiques associatifs impairs. Principe basé sur la méthode de De la Hire	Principe 1 Deux matrices l'une avec les nombres de 1 à 5 et l'autre avec les nombres multiples de 5 de 0 à 25. Le carré magique est la somme des deux matrices. Matrice = tableau = grille Principe 2 Placement des nombres aux sommets des carrés de façon à satisfaire l'associativité. Principe 3 Choix du placement de cinq nombres dans chaque matrice de façon équilibrée (ou symétrique). L'idée est de satisfaire le caractère associatif du carré: la somme de deux nombres symétriques par rapport au centre est constante: (n² + 1). Principe 4 Choix du placement des autres nombres.
Exemple avec le carré d'ordre 5: Nombres utilisés: de 1 à 25. Somme magique: 25 x 26 / 2 / 5 = 65 Nombre central: (25 +1)/2 = 13. Somme associative: 25 + 1 = 26		Une des solutions

Voir Carré magique 5x5

Principe 1 – Somme
Comment obtenir les nombres de 1 à 25 en additionnant deux nombres pris dans les deux ensembles (1, 2, 3, 4, 5) et (0, 5, 10, 15,20)	Table d'addition

Principe 2 – Travailler les coins
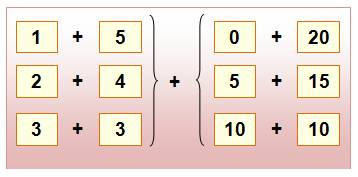
Dans tous les cas, les sommes des sommets en diagonale doit être 26.	Un exemple de sommes possibles (2 + 4) + (20 + 0) = 26 (1 + 5) + (15 + 5) = 26
Toutes les sommes 26 possibles en tant que sommes des quatre nombres sur les deux matrices? Seules possibilités: faire 6 avec la première matrice, et faire 20 avec la seconde.	Seules possibilités pour faire 26

Principe 3 – Configuration symétrique
Le nombre central du carré magique associatif est 13; soit 3 et 10 pour les deux matrices On place cinq fois ces deux nombres: de façon symétrique dans la première grille. en position miroir dans l'autre (symétrie verticale). À ce stade, la somme de ces deux matrices donne un carré "magique" de somme 13.

Principe 4 – Dernier choix et finalisation
Première matrice Le 3 étant placé, reste deux couples à distribuer: l'un sur une diagonale (2, 4), et le second sur l'autre (1, 5). Seconde matrice Le 10 étant placé, reste deux couples à distribuer: l'un sur une diagonale (0, 20), et le second sur l'autre (5, 15). Remplissage Le 2 en haut à gauche précède le 3. On applique cet ordre sur les autres lignes. Le 4 en bas à droite suit le 3. On applique cet ordre sur les autres lignes. Ensuite, le 5 précède le 1 et suit le 4, etc. Même méthode pour remplir la seconde matrice.
Carré magique Il est obtenu en faisant la somme des deux nombres qui se correspondent dans les deux matrices. Par exemple: 2 + 20 = 22.

Exemple 5x5
Symétrie en jaune Nombres des sommets en rouge. Le 3 étant placé un coin laisse la liberté d'inverser le 2 et le 4.

Exemple 7x7
Exemple avec le carré d'ordre 7: Nombres utilisés: de 1 à 49. Somme magique: 49 x 50/ 2 / 7 = 175 Nombre central: (49 +1)/2 = 25. Somme associative: 49 + 1 = 50 Matrice A: (1, 2 3, 4, 5, 6, 7) Matrice B: (0, 7, 14 21, 28, 35, 42) Symétrie en jaune (nombreux choix). Nombres des sommets en rouge (nombreux choix). Nombreuses possibilités également pour le choix des autres nombres. Mais, un fois le choix effectué, on respecte le même ordre sur les lignes, et cela, sur les deux matrices. Deuxième exemple	Seules possibilités pour faire 50 Construction du carré

Voir Carré magique 7x7

Suite	Carré à échelle alternée – Vers les carrés de Franklin Carrés magiques – Index Construction matricielle des carrés magiques Carré latins et constructions de carrés magiques Relations mathématiques dans le carré3x3 Relations mathématiques dans le carré 4x4 Relations mathématiques dans le carré 5x5 Symétries dans le carré magique
Voir	Jeux – Index Jeux de nombres – Index Jeux numériques – Index Rectangles magiques
Sites	Voir page spéciale
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Symetrie.htm