|
||||||||||||||||||||||||||||||||
![]()
|
Mathématiques des Carrés Magiques Les carrés gréco-latins ou carrés latins orthogonaux Une façon
simple de construire des carrés magiques consiste à superposer
deux carrés latins orthogonaux (carré gréco-latin),
à condition que les nombres utilisés soient aussi uniques sur les deux
diagonales. |
|
|
Les carrés orthogonaux sont faciles à construire
pour les ordres impairs: Il existe une règle simple
pour n premier |
Pour les ordres pairs,
Ce qui ne veut pas dire qu'il n'existe pas de carrés magique d'ordre 6. |
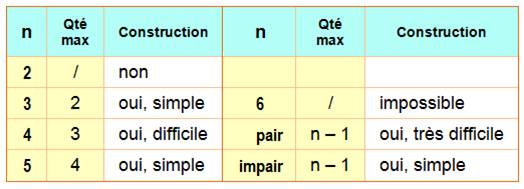
En résumé
![]()
ORDRE IMPAIR
|
|
||
|
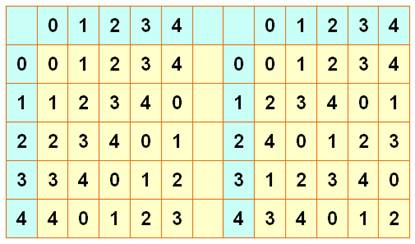
À gauche un carré latin d'ordre 5. Chaque cellule
vaut: G (Sorte de table
d'addition) Le carré latin de droite lui est orthogonal via l'introduction du facteur 2: chaque cellule vaut: D Avec k = 1, 2, 3 et 4
on obtient les quatre carrés latins mutuellement orthogonaux d'ordre 5 Modulo
5 veut dire que l'on ne garde que le reste de la
division par 5 >>> |
Tables d'addition particulières en modulo 5
Pour tout carré d'ordre premier,
la superposition de ces deux carrés latins orthogonaux
produit un carré gréco-latin. Notez que cette création n'assure
pas la condition d'unicité de répartition sur les diagonales. Dit-autrement:
les cinq carrés latins créés par cette méthode n'engendrent pas un carré
magique. |
|
|
Démonstration Soit deux paires: Si même paire: Soustraction: |
Modulo 2n + 1: (x + y, 2x + y) et (x' + y', 2x' + y'). x + y = x' + y'
et 2x + y = 2x' + y' x = x' et alors y =
y' Toutes les paires
son distinctes. |
|
![]()
ORDRE PAIR
|
|
||
|
La
construction des carrés gréco-latins d'ordre pair est plus problématique.
Trois cas sont à distinguer:
|
Pour
l'ordre pair, il existe une technique semblable à celle des impairs, dite du
modulo généralisé. Elle introduit la solution imaginaire de l'équation x² + x
+ 1 (Extension des nombres au corps finis de Galois). |
|
|
|
|
|
Il existe des carrés gréco-latins d'ordre quelconque, sauf pour 2 et 6. Il a fallu attendre les années 1950 pour prononcer cette affirmation.
Euler publie deux papiers sur
ce sujet: En 1776, De Quadratis Magicis, où il énonce les propriétés des
carrés gréco-latin et où il montre qu'ils peuvent donner naissance à des
carrés magiques via un algorithme très simple. Ce papier de sept pages est
sans doute le premier article sur les carrés magiques dans leur généralité. Le second papier, Recherches sur une nouvelle espèce de carrés
magiques, est publié en 1782. C'est le premier traité écrit à propos des
carrés gréco-latins. Euler trouve une méthode pour construire des carrés gréco-latins
d'ordre impair et d'ordre multiple de
4. Il est incapable d'en construire pour n = 2 ou n =
6, il conjecture
qu'ils n'existent pas pour n = 4k + 2, comme 6, 10, 14 … En 1842, Thomas Clausen vérifie la non-faisabilité du 6x6 en
réduisant le problème à l'analyse de 17 cas fondamentaux. Il ne publie pas. En 1901, Gaston Tarry montre la
non-existence pour n = 6. À la main, il examine tous les cas
possibles: 9 408 carrés (en fait une quantité réduite à partir des 812 851
200 possibles). Stinson donnera la preuve formelle en 1984. En 1902, les cas de 10, 14 …sont prouvés, mais avec des erreurs, par
Petersen, puis Wernicke en 1910 et
encore par MacNeish en 1922. En 1957, Paige et Tompkins cherchent un 10x10
sur ordinateur. Sans résultat, mais une prédiction que le temps d'exploration
serait hors de portée des ordinateurs
actuels. En 1959, Bose et
Shrikhande arrivent à produire un carré d'ordre 22. Puis Parker en trouve un d'ordre 10 à l'aide
d'une exploration par ordinateur. Ensemble, les trois publient un papier
montrant que les carrés gréco-latins existent toujours pour n>2 à
l'exception de n = 6. |
|
|
|
||
|
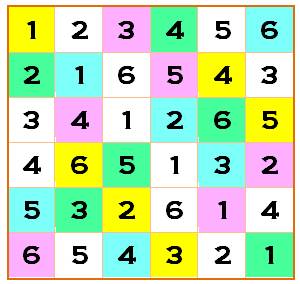
Tentative pour l'ordre 6 Les
quatre sextuplets de couleur représente chacun une transversale.
Exemple trouvé
par Finney (1945). Avec l'ordre
6, on sait qu'il est impossible de compléter ce carré latin avec deux autres
sextuplets disjoints qui produirait un carré orthogonal au premier. Le carré latin orthogonal à un autre d'ordre n possède n transversales
disjointes. Euler utilisait ce concept pour élaborer ses carrés gréco-latins. Il est impossible de remplir les cases blanches avec
deux nouvelles transversales. |
Carré latin avec quatre transversales identifiées
|
|
|
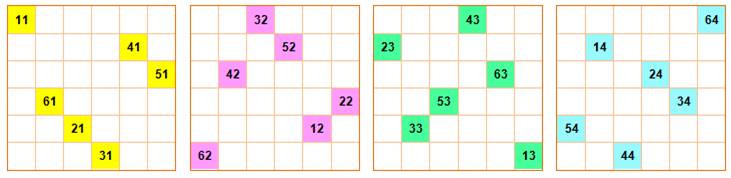
Les quatre transversales isolées (pour
information
Note: une diagonale
de carré latin d'ordre n doit être entendue comme un ensemble de n cellules
représentatives de chaque ligne et de chaque colonne (une diagonal en
"vrac"). Un transversale est une diagonale sans répétition des
nombres. Tentatives de recherches de nouvelles
transversales La grille
avec les transversales trouvées. En blanc, les choix possibles pour les deux
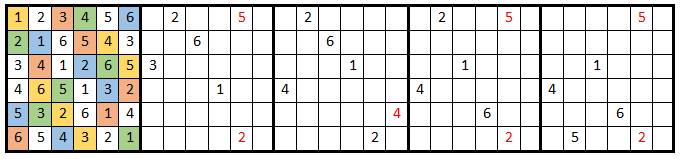
dernières. Les quatre grilles suivantes montrent les tentatives possibles qui
aboutissent à des impossibilités. Dans le premier cas, en colonne 5, il faut
placer un 2 doublon) ou un 5 (ligne déjà occupée. Échec.
Erratum: la
case ligne 3 colonne 4 de la deuxième tentative est un 1 au lieu d'un 2.
Merci O. Guilot |
||
Intérêt mathématique des
transversales des carrés latins
|
Ce sujet est traité sur la première
page relative aux carrés latins. Selon que le carré latin est complet ou non en
transversales, ils possèdent des propriétés mathématiques différentes:
notions de carrés latins mutuellement orthogonaux (MOLS). Effectivement, les carrés latins sont un sujet d'études des
mathématiques avancées, et cela, du fait de leurs nombreuses applications
notamment en cryptographie, code auto-correcteur d'erreurs, en mécanique
quantique carrés latins quantiques), etc. Le carré latin, un sujet banal mais qui conduit à des développements
en mathématiques très avancées. |
|
|
||
|
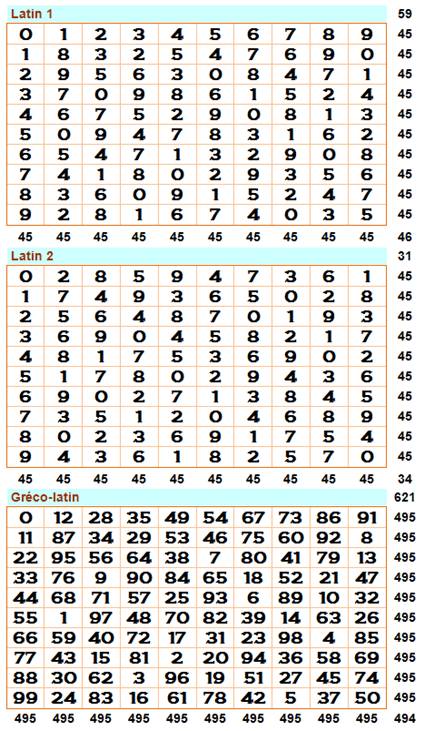
Il s'agit ici du premier carré gréco-latin
construit par Paker en 1963. Le carré latin 1 est celui qui a servi de point
de départ à Paige et Tompkins. Sans perte de généralité, la première colonne du
latin 2 à trouver p est fixée avec la suite des nombres. La première approche consiste à prendre les cases
un par un. Après le 0, ne peur pas venir le 1 qui est déjà à cette place dans
le latin1. Avec cette méthode on pourrait placer 0214365897 sur la première ligne.
Cette approche s'essouffle même avec ordinateurs.
Il faut trouver autre chose. Revenir à la méthode des transversales d'Euler. Ce que fit Parker. Il s'agit d'identifier toutes les transversales
(lignes potentielles) possibles. Dans le cas présent, il y en a exactement
808. Le tout est alors de trouver les 10 qui se placent correctement dans le
carré. Un problème à la portée de nos ordinateurs actuels. L'astuce est très bénéfique en temps de calcul
transformant la quantité de calcul fonction d'un produit en une fonction de
sommes. |
|
|
|
On sait que pour
qu'il existe un ensemble complet de carrés latin mutuellement orthogonaux
pour l'ordre pk, p étant premier. On ne sait pas le dire pour les
autres cas. Pour n = 10, on ne sait pas la quantité. La quantité de carrés
latins est bien trop importante pour procéder à un test exhaustif par
ordinateur. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Grelatin.htm
|
![]()