NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 16/10/2015

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

     

Carrés magiques

 

Débutants

Carrés

magiques

Carré magique 5 x 5

 

Glossaire

Carrés

magiques

 

 

INDEX

 

Carrés magiques

 

Jeux

Carré 5 x 5

Construction

Diaboliques

Générique

Propriétés

Premiers

Sommaire de cette page

>>> Formules génériques pour l'ordre 5

>>> Formules de Lee Sallow

>>> Formules pour le carré magique pandiagonal

 

 

 

 

Carrés magiques d'ordre 5

Formulation générique

 

Quelles sont les formules qui produisent un carré magique, et quel est le nombre minimal de variables indépendantes?

 

 

 

 

FORMULES GÉNÉRIQUES – Ordre 5

Formules générales

 

Avec 14 variables indépendantes:

 

F, G, I, J,

N, O,

Q, R, S, T,

V, W, X, Y.

 

 Et 11 variables liées.

A

B

C

D

O

E

F

G

H

P

I

J

Q

R

S

K

L

T

M

N

U

V

W

X

Y

 

Formules génériques générales

 

Constante

A

B

C

D

E

F

G

H

I

J

K

L

M

N

Autres

O =

65

– A

– B

– C

– D

 

 

 

 

 

 

 

 

 

 

 

P =

65

 

 

 

 

– E

– F

– G

– H

 

 

 

 

 

 

 

T =

65

 

 

 

 

 

 

 

 

 

 

– K

– L

– M

– N

 

U =

65

– A

 

 

 

– E

 

 

 

– I

 

– K

 

 

 

 

V =

65

 

– B

 

 

 

– F

 

 

 

– J

 

– L

 

 

 

Q =

65

 

 

 

 

 

 

 

– H

 

 

 

– L

 

 

– U – O

=

– 65

+ 2A

+ B

+ C

+ D

+ E

 

 

– H

+ I

 

+ K

– L

 

 

 

Y =

65

– A

 

 

 

 

– F

 

 

 

 

 

 

– M

 

– Q

=

2 x 65

– 3A

– B

– C

– D

– E

– F

 

+ H

– I

 

– K

+ L

– M

 

 

S =

65

 

 

 

 

 

 

 

 

 

 

 

 

 

– N

– O – P – Y

=

– 3 x 65

+ 4A

+ 2B

+ 2C

+ 2D

+ 2E

+ 2F

+ G

 

+ I

 

+ K

- L

+ M

– N

 

R =

65

 

 

 

 

 

 

 

 

– I

– J

 

 

 

 

– Q – S

=

5 x 65

– 6A

– 3B

– 3C

– 3D

– 3E

– 2F

– G

+ H

– 3 I

– J

– 2K

+ 2L

– M

+ N

 

X =

65

 

 

 

– D

 

 

 

– H

 

 

 

 

– M

 

– R

=

– 4 x 65

+ 6A

+ 3B

+3C

+ 2D

+ 3E

+ 2F

+ G

– 2H

+ 3 I

+ J

+ 2K

– 2L

 

– N

 

W =

65

 

 

 

 

 

 

 

 

 

 

 

 

 

 

– U – V – X – Y

=

65

– 2A

– B

– 2C

– D

– E

 

– G

+ H

– I

 

 

+ 2L

+ M

+ N

 

                                                                                                                                         

 

Formules de Lee Sallow

15 variables indépendantes

A + a + x

B + b – z

C + c – v – x + z

D

E + d + v

C

D + d – x

E + a + v + x + y

A + b – v

B + c – y

E + b – u – x – y

A + c + u + x + z

B

C + d + v + w – z

D + a – v – w + y

B + d + y

C + a – u

D + b + u + w – y

E + c – w

A

D + c + u

E

A + d – u – w – z

B + a + z

C + b + w

 

 

Mise sous tableur de ces formules

 

On donne les valeurs suivantes

 

A

B

C

D

E

a

b

c

d

u

v

w

x

y

z

3

13

23

8

18

– 2

2

1

–1

0

0

0

0

0

0

 

 

On forme le tableau avec les valeurs des grandes lettres

C'est un carré latin qui est aussi magique de somme 65.

 

 

3

13

23

8

18

23

8

18

3

13

18

3

13

23

8

13

23

8

18

3

8

18

3

13

23

Et celui des sommes algébriques des petites lettres

C'est un carré latin qui est aussi magique de somme nulle.

 

 

-2

2

1

0

-1

0

-1

-2

2

1

2

1

0

-1

-2

-1

-2

2

1

0

1

0

-1

-2

2

Maintenant la somme des deux

C'est un nouveau carré magique de somme 65.

Celui-ci est un carré normal, formé de tous les nombres de 1 à 25.

C'est celui de la première page sur les carrés magique 5 x5.

 

1

15

24

8

17

23

7

16

5

14

20

4

13

22

6

12

21

10

19

3

9

18

2

11

25

 

 

 

 

Formules pour un carré pandiagonal

8 variables indépendantes

A

B

C

D

65 – A – B

– C – D

F

G

H

I

65 – F – G

– H – I

 –  A + H + I

65 – B – F

– G – H

65 – C – G

– H – I

 –  D + F + G

– 65 + A + B +

C + D + G + H

65 – C – D

– H – I

 – 65 + A + B +

C + F + G + H

 – 65 + B + C +

D + G + H + I

65 – A – B

– F – G

65 – B – C

– G – H

C + D – F

65 – A – B

– C – G

65 – B – C

– D – H

A + B – I

 – 65 + B + C +

F + G + H + I

 

Le carré ci-dessus répond à ces formules; il est pandiagonal.

 

 

Formules pour un carré pandiagonal

10 variables indépendantes

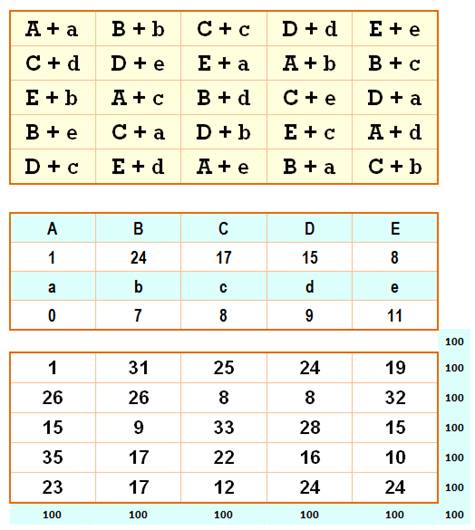
Les formules très sobres! Combinaisons de deux variables seulement.

 

 

Un exemple avec choix des dix variables.

 

 

 

Le carré est magique et panmagique de somme 100. Il comporte les nombres:

1, 8, 8, 9, 10, 12, 15, 15, 16, 17, 17, 19, 22, 23, 24, 24, 25, 26, 26, 28, 31, 32, 33, 35.

Avec de nombreux doublons.

 

Les formules semblent sympathiques mais sont loin de donner les solutions pour un vrai carré magique.

 

 

 

 

 

 

 

 

 

Suite

*    Carré d'ordre 6 et plus

*    Carrés magiques – Index

Voir

*    Carrés – les nombres

*    Carrés en géométrie

*    Carrés mystérieux

*    Dominos magiques

*    Énigmes

*    Géométrie

*    Humour

*    Jeux

*    Jeux  de  chiffres

*    Nombres consécutifs

*    Nombres en chiffres

*    Nombres magiques - Index

*    Pannumérique

*    Paradoxes

*    Propriétés du carré magique

*    Rubriques débutants

*    Sudoku

Diconombre

*    Nombre 5

*    Nombre 25

*    Nombre 65

Sites

*    Liens vers les sites carrés magiques

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordr52.htm