Partition des nombres avec les nombres de 1 à 9

Édition du: 06/03/2025

INDEX Partition Calculs	PARTITIONS
	Approche	En bref et Index	S'y retrouver
	Formules de récurrence	Quantité de partitions	Partielles (1/2) – (2 / 2)
	Partitions palindromiques	Partitions non-croisées	Partitions pannumériques
	Partitions avec 1 à 9

Faites un double-clic pour un retour en haut de page

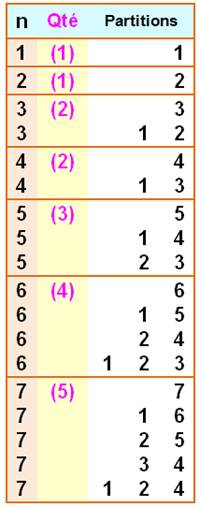
PARTITIONS

avec des nombres distincts de 1 à 9

Quelles sont les additions des nombres parmi 1 à 9 qui produisent des sommes identiques et égale à un nombre donné n ?

Sommaire de cette page

>>> Premières partitions

>>> Exemples

>>> Quantité de partitions 1-9

>>> Les 23 partitions 1-9 des nombres de 21 à 24

>>> Partitions 1-9 avec consécutifs

Débutants

Addition

Glossaire

Addition

Premières partitions

haut

Sommes

Nous cherchons à énumérer les partions des nombres de 1 à 10 en utilisant les nombres de 1 à 9 seulement et cela une seule fois.

Soit: toutes les additions de nombres distincts de 1 à 9 pour obtenir les sommes de 1 à 10.

Nombre 10

Il existe neuf telles partitions pour atteindre le nombre 10.

Nombres consécutifs

Hors cas trivial (comme 4 = 1 + 3), les partitions avec des nombres consécutifs sont les suivantes:

6 = 1 + 2 + 3
7 = 3 + 4
9 = 4 + 5
10 = 1 + 2 + 3 + 4

Exemples		haut
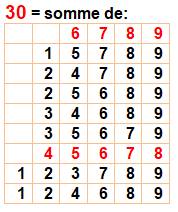
Le nombre 30 est dix-sept fois somme de nombres parmi 1 à 9.
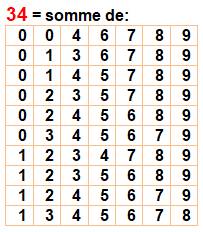
Le nombre 34 est dix fois somme de nombres parmi 1 à 9.
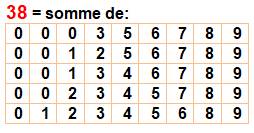
Le nombre 38 est cinq fois somme de nombres parmi 1 à 9.
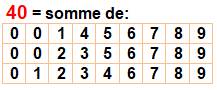
Le nombre 40 est trois fois somme de nombres parmi 1 à 9.

Voir Nombre 30 / Nombre 34 / Nombre 38 / Nombre 40

Quantité de partitions 1-9

haut

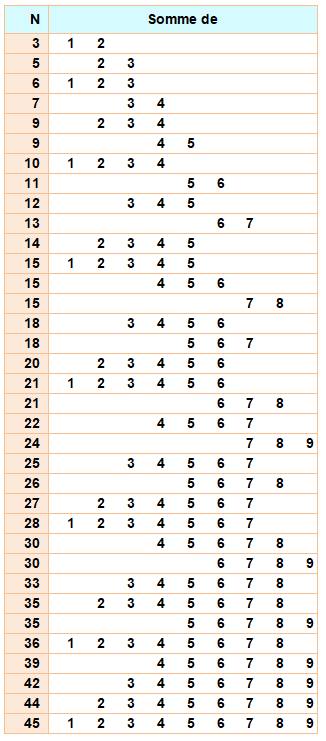
Maximum de partitions 1-9 pour les nombres de 21 à 24.

Aucune partition 1-9 à partir de 45. Logique car 45 épuise tous les nombres de 1 à 9:
45 = 1 + 2 + 3 + 4 + 5 + 6 + 6 + 7 + 8 + 9.

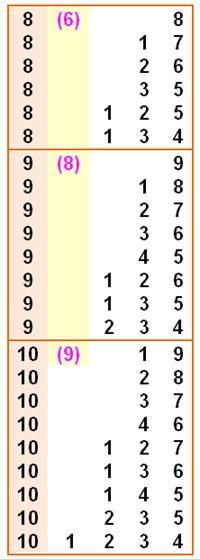
[nombre n, quantité de partitions 1-9]

[1, 1], [2, 1], [3, 2], [4, 2], [5, 3], [6, 4], [7, 5], [8, 6], [9, 8], [10, 9], [11, 10], [12, 12], [13, 13], [14, 15], [15, 17], [16, 18], [17, 19], [18, 21], [19, 21], [20, 22], [21, 23], [22, 23], [23, 23], [24, 23], [25, 22], [26, 21], [27, 21], [28, 19], [29, 18], [30, 17], [31, 15], [32, 13], [33, 12], [34, 10], [35, 9], [36, 8], [37, 6], [38, 5], [39, 4], [40, 3], [41, 2], [42, 2], [43, 1], [44, 1], [45, 1], [46, 0], [47, 0], [48, 0], [49, 0], [50, 0], …

Les 23 partitions 1-9 de chacun des nombres de 21 à 24

En rouge, les partitions en nombres consécutifs

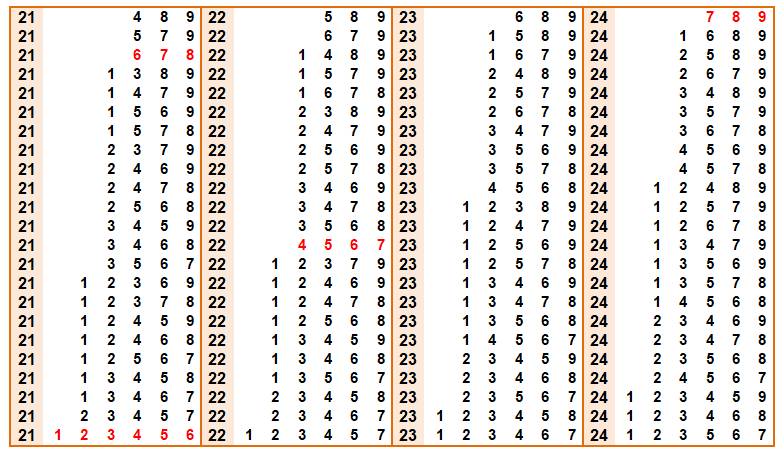
Voir Nombre 21 / Nombre 22 / Nombre23 / Nombre 24

Partitions 1-9 avec consécutifs

haut

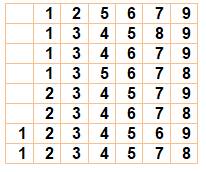
Tableau des 35 sommes de nombres consécutifs parmi les nombres de 1 à 9.

La plus grande étant évidemment:
45 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9

Les nombres non atteints par de telles sommes sont:
2, 4, 8, 16, 17, 19, 23, 29, 31, 32, 34, 37, 38, 40, 41, 43.

Haut de page (ou double-clic)

Retour	Partition – Introduction
Suite	Partition – S'y retrouver Partitions – Formules de récurrence Partition {2, 3} – Système à double base
Voir	Addition - Glossaire Addition des carrés Addition des entiers Addition des puissances Carrés magiques Multi-somme de puissances
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/Pttnb1a9.htm