NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/09/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	THÉORIE DES NOMBRES
Débutants Général	DIVISEURS ET MULTIPLES			Glossaire Général
INDEX Calcul Théorie des nombres	PGCD	PPCM	Premiers entre eux
	Algorithme d'Euclide	Sa programmation	PGCD / PPCM / Racine
		Sommaire de cette page >>> Algorithme d'Euclide >>> Disposition pratique >>> Exemple expliqué >>> Démonstration >>> Préparation de la programmation >>> Organigramme >>> Programme >>> Formation d'une expression linéaire

ALGORITHME D'EUCLIDE

pour le calcul du PGCD

Plus Grand Commun Diviseur

Description de l'algorithme d'Euclide.

Exemple de présentation d'un algorithme.

Voir Algorithme d'Euclide (Terminale)

ALGORITHME D'EUCLIDE
Il s'agit de divisions en cascade: les résultats de l'une servent à poser la suivante: Le diviseur B devient le dividende; et Le reste r1 devient le diviseur. Arrêt lorsque le reste de la division est nul. Le reste trouvé avant le reste nul est le PGCD des nombres A et B.

Disposition pratique
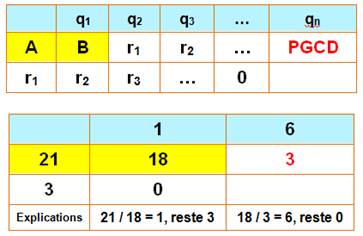
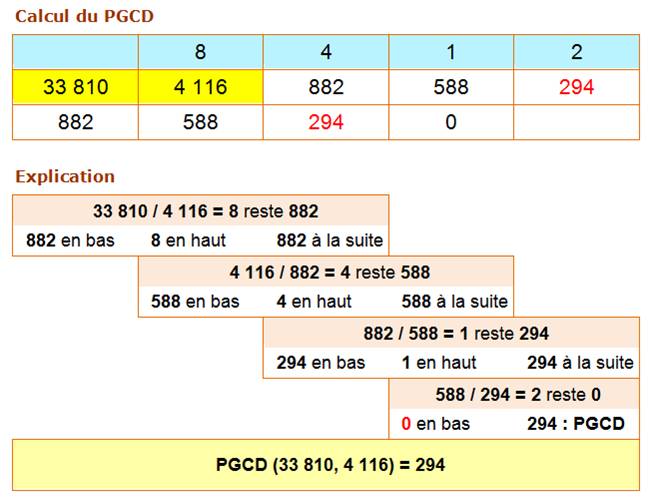
Au lieu de mettre le quotient q en bas, on le place au-dessus du diviseur de manière à laisser la place au reste de la division suivante.	Principe et exemple

Exemple complet expliqué
A = 33 810 = 1 x 2 x 3 x 5 x 7 x 7 x 23 B = 4 116 = 1 x 2 x 3 x 7 x 7 x 7 PGCD (A, B) = 1 x 2 x 3 x 7 x 7 = 294

Démonstration On note: g = PGCD(A, B) avac A >B
Départ	Division de A par B.	A = Bq + r
1 – Cas n°1
Si r = 0	Alors B divise A.	g = B
2 – Cas n°2
Si r 0	Si g existe, il divise A (a= g.a) et B (B=g.b) Or, tout diviseur g, commun à A et B, divise aussi r, selon la démonstration ci-contre.	A – Bq = r g.a – g.b.q = r g(a – b.q) = r g(a – b.q) = g.s r = g.s
Autrement dit	Tout diviseur g, commun à B et r, divise aussi A.	Bq + r = A
31 – Nouveau problème
	Cherchez les diviseurs communs à B et r. Tous deux sont plus petits que les nombres A et B initiaux. Le problème est simplifié.	r < B < A
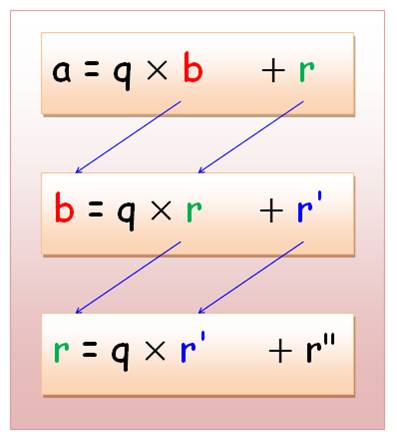
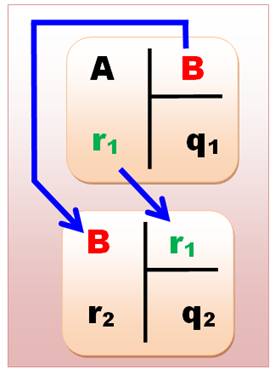
Poursuivons	On réalise les divisions successives. Les restes vont en diminuant.	A = Bq + r B = rq1 + r1 r = r1 q2 + r2 r1 = r2 q3 + r3 … rn-1 = rn qn+1 + rn+1
32 – Deux cas possibles
Si rn+1 = 0	Les diviseurs cherchés sont ceux de rn	rn divise rn-1
	Et …	g = rn
Si rn+1 = 1	Les diviseurs communs à A et B sont les diviseurs communs à rn et à 1.	A et B sont premiers entre eux. g = 1.

RAPPEL pour préparer la programmation

Rappel du principe avec ces exemples

La division de A	par B	donne un reste R
8 136	492	264
492	264	228
264	228	36
228	36	12
36	12	0

On a bien:

8 136 = 12 x 678

492 = 12 x 41

La division de A	par B	donne un reste C
123 456 789	467 769	433 542
467 769	433 542	34 227
433 542	34 227	22 818
34 227	22 818	11 409
22 818	11 409	0

On a bien

123 456 789	= 11 409	x 10 821
467 769	= 11 409	x 41

On note la simplicité

À chaque ligne suivante:

A prend la valeur de B,

B celle de R.

Et, on recommence la division avec ces nouvelles valeurs de B et R.

On s'arrête lorsque R est nul.

Le PGCD est égal au B final.

Illustration

ORGANIGRAMME
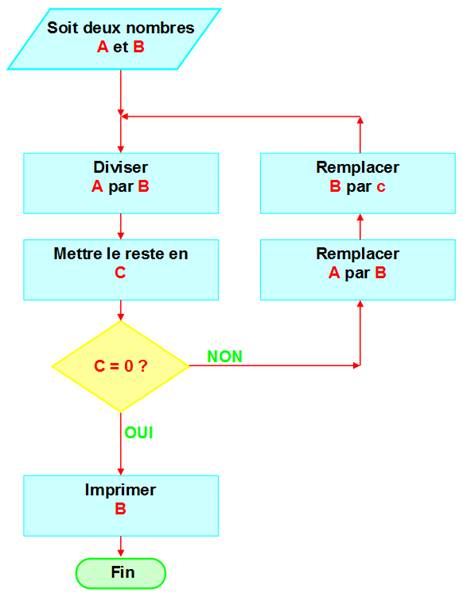
Organigramme - Anglais: flow chart Les symboles utilisés ici sont les plus courantes. Les rectangles correspondent à des ordres à exécuter. On parcourt les instructions dans le sens des flèches. Les aiguillages sont symbolisés par un losange. On emprunte la flèche qui correspond au résultat du test.

PROGRAMME selon l'organigramme ci-dessus
A := 8136: B := 492: C := 1: while C<>0 do C := A mod(B): lprint(A,B,C): A := B: B := C: od: 8136, 492, 264 492, 264, 228 264, 228, 36 228, 36, 12 36, 12, 0 Autre exemple d'exécution 454545545454, 531441, 338067 531441, 338067, 193374 338067, 193374, 144693 193374, 144693, 48681 144693, 48681, 47331 48681, 47331, 1350 47331, 1350, 81 1350, 81, 54 81, 54, 27 54, 27, 0	Le calcul du reste de la division est remplacé par son équivalent : le calcul du modulo: C = A modulo B. (C est alors le reste de la division de A par B) On imprime le résultat à chaque itération pour obtenir le résultat présenté comme indiqué ci-dessus. Notez que: L'instruction while se poursuit tant que C est différent de 0. Il est donc important de lancer le programme avec une valeur de C différente de 0. Ici, on a choisi de forcer C à 1.
Langage type Maple: voir Convention de notations / Programmation

Exemple avec expression linéaire
Appliquez l'algorithme d'Euclide pour trouver:	g = PGCD (2059, 2581) = ? g = f(2059, 2581) = ?
Suite des opérations.
PGCD	g = 29
En remontant la chaine.

Voir Théorème de Bachet-Bézout – Identité de Bézout

Efficacité

1,467 078 079 4 … Constante de Porter

Elle caractérise l'efficacité de l'algorithme d'Euclide.

Notion avancée

Suite	Algorithme d'Euclide (page voisine) PGCD / PPCM / Racine Calcul des fractions continues
Voir	Algorithmes Diviseurs: calculs et facteurs premiers Division Théorie des nombres
Cette page	http://villemin.gerard.free.fr/ThNbDemo/AlgoEucl.htm