NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/05/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Théorie des Nombres
Débutants Division	DIVISIBILITÉ			Glossaire Division
INDEX Accueil Sommaire	Approche	Divisible	Division
		Div. commun	Applications
		Sommaire de cette page >>> Méthode de calcul >>> Cas simple >>> Cas intermédiaire >>> Cas général

Division – Applications

PGCD (Plus Grand Commun Diviseur)

& Algorithme d'Euclide ou théorème d'Euclide

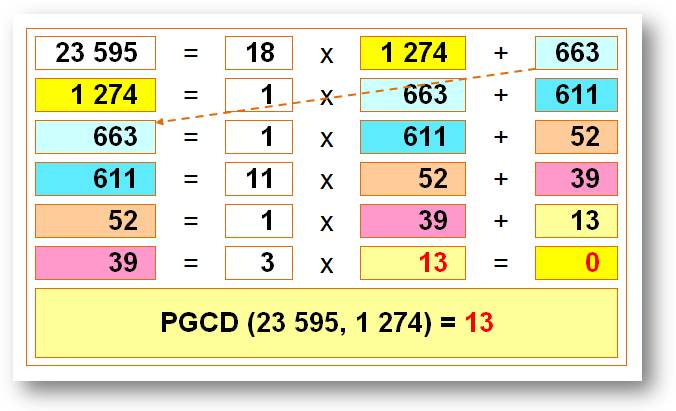
Comment trouver le plus grand facteur commun à deux nombre en utilisant l'algorithme d'Euclide.

Nous avons vu que le PGCD (g) est tel que g = a.u + b.v

Connaissant deux nombres a e b, comment claculer g, u et v ?

Voyons la théorie et le procédé correspondant. Voici d'abord un calcul tout fait pour observer et se donner une idée.

Observation du procédé pour calculer un PGCD
Algorithme d'Euclide pour 23 595 et 1 274 Les couleurs montrent comment les nombres se propagent OK! Il y a plusieurs divisions successives et je vois bien comment elles s'enchaînent. Par contre, je ne comprends pas comment on obtient ces valeurs!

Cas simple

Exemple:

a	=		3	x 5	=	15
b	=	2	x 3		=	6

Marche avant: recherche de g

D'après le théorème page précédente.

(a, b)

= (a – m.b, b)

Application numérique:

On prend m le plus grand possible (ici m = 2), tout en conservant un résultat positif.

On constatera qu'il s'agit, évidemment,
du quotient de la division de a par b.

(15, 6)

= (15 – (2) 6, 6)

= (3, 6)

= 3

Le résultat est immédiat: le PGCD de (15 et 6) est 3.

(15, 6)

= 3

Cas intermédiaire

Exemple:

a	=		5 x 7	x 11	=	385
b	=	3	x 5 x 7		=	105

Marche avant: recherche de g

D'après le théorème:

(a, b)

= (a – m.b, b)

Application numérique.

(385, 105)

= ((1) 385 + (– 3) 105, 105)

= (70, 105)

Recommençons avec les nouvelles valeurs.

(105, 70)

= ((1) 105 + (–1) 70, 70)

= (35, 70)

= 35

Résultat:

(385, 105)

= 35

Marche arrière: recherche de x et y

Effectuons la marche arrière.

70

35

= (1) 385 + (–3) 105

= (1) 105 + (–1) 70

= (1) 105 + (–1) {(1) 385 + (–3) 105}

= (–1) 385 + (4) 105

Valeurs de x et y:

x

y

= –1

= 4

Cas général

Exemple:

a	=	3 x 5 x 11²	x 13	=	23 595
b	=	2 x 7²	x 13	=	1 274

Voir Illustration

Marche avant: recherche de g

D'après le théorème:

(b, c)

= (b – m.c, c)

Application numérique.

(23 595, 1 274)

= ((1) 23 595 + (–18) 1 274, 1 274)

= (663, 1 274)

Recommençons avec les nouvelles valeurs.

(1 274, 663)

= ((1) 1 274 + (–1) 663, 663)

= (611, 663)

Encore.

(663, 611)

= ((1) 663 + (–1) 611, 611)

= (52, 611)

"

(611, 52)

= ((1) 611 + (–11) 52, 52)

= (39, 52)

"

(52, 39)

= ((1) 52 + (–1) 39, 39)

= (13,52)

= 13

Résultat:

(23 595, 1 274)

= 13

Marche arrière: recherche de x et y

Effectuons la marche arrière

Le premier retour est souligné en vert.

663

= (1) 23 595 + (–18) 1 274

Pour le suivant, on prend
la ligne en dessous.

Et on développe avec
les quantités connues (en vert).

611

= (1) 1 274 + (–1) 663

= (1) 1 274 + (–1) {(1) 23 595 + (–18) 1 274}

= (–1) 23 595 + (19) 1 274

Idem.

52

= (1) 663 + (–1) 611

= (1) { (1) 23 595 + (–18) 1 274}

+ (–1) {(–1) 23 595 + (19) 1 274}

= (2) 23 595 + (–37) 1 274

"

39

= (1) 611 + (–11) 52

= 1) {(–1) 23 595 + (19) 1 274}

+ (–11) {(2) 23 595 + (–37) 1 274}

= (–23) 23 595 + (426) 1 274

"

13

= (1) 52 + (–1) 39

= (1) { (2) 23 595 + (–37) 1 274}

+ (–1) {(–23) 23 595 + (426) 1 274}

= (25) 23 595 + (–463) 1 274}

Valeurs de x et y:

x

y

= 25

= – 463

Bilan

Nous savons calculer le PGCD en utilisant l'algorithme d'Euclide et

nous savons aussi trouver les coefficients de l'expression g = a.x + b.y

Nous allons maintenant nous consacrer aux diviseurs d'un nombre donné. Combien y en a-t-il ?

Suite	Facteurs et diviseurs Autre exemple de calcul
Autour	Algorithme d'Euclide et sa programmation Notion de diviseurs communs PGCD - PPCM La division en pratique c'est quoi? – Débutant La division en résumé c'est quoi? – Glossaire Divisibilité par un nombre donné
Voir	Cryptage Des jeux sur les partages Jeux et puzzles – Index L'arithmétique de l'horloger Le calcul mental Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/Referenc/Prof/APROF/DivEucli.htm