NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/05/2015 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	TOPOLOGIE
Débutants Géométrie	QUATRE COULEURS Divers				Glossaire Géométrie
INDEX Quatre couleurs Géométrie Topologie	Général	Historique	Prince de Möbius	Diamant de Birkhoff
		Sommaire de cette page >>> Les cinq princes de Möbius >>> Les cinq palaces de Tietze >>> Les cinq régions de De Morgan >>> Bilan

Les cinq princes de Möbius

Énigme de partage de pays avec mitoyenneté qui préfigure le problème de quatre couleurs.

Émise en 1840 par August Möbius (1790-1868), astronome à Leipzig, inventeur du ruban éponyme.

Les cinq princes de Möbius
Un roi Indien avait cinq fils. Sa dernière volonté est de partager son royaume entre ses fils de telle sorte que la région de chacun ait une frontière commune (pas seulement un point) avec les quatre autres. Comment s'y prendre?	Möbius aurait donné cet exercice à ses élèves et se serait amusé de les voir s'efforcer à résoudre ce problème. Finalement, il leur avoue que ce problème est infaisable.
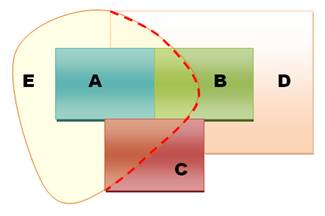
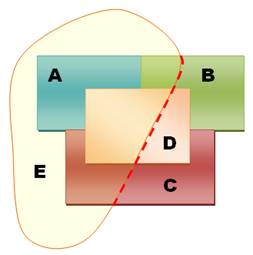
L'argument de Möbius est relativement simple tel que vu sur les figures à droite. Disposer trois régions (A, B et C) toutes mitoyennes entre elles ne pose pas de problème. Ajouter une quatrième non plus, mais deux possibilités: la quatrième est externe ou interne. Dans les deux cas, impossible d'ajouter une cinquième région sans empiéter sur els autres (pointillé rouge).
Heinrich Tietze (1880-1964), mathématicien autrichien, propose une variante: les cinq palais: Les princes devront relier leur palais (leur capitale) deux à deux sans que les routes se croisent.	Il s'agit de la question duale de celle proposée précédemment pour laquelle la topologie de régions est transformée en graphe. Ce problème n'a pas plus de solution, bien entendu.
En 1852, De Morgan prouvera proprement cette affirmation:	Il est impossible de disposer cinq régions de telle façon qu'il existe des frontières communes entre tous les couples possibles.

Les cinq palaces de Tietze
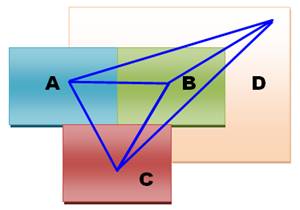
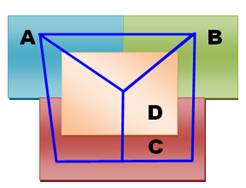
Heinrich Tietze (1880-1964), mathématicien autrichien, propose une variante: les cinq palais: Les princes devront relier leur palais (leur capitale) deux à deux sans que les routes se croisent.	Il s'agit de la question duale de celle proposée précédemment pour laquelle la topologie de régions est transformée en graphe. Ce problème n'a pas plus de solution, bien entendu.
En reprenant les deux cas de figures vus ci-dessus, on constate que réunir les capitales deux à deux consiste à dessiner le graphe complet entre quatre points. Ajouter un cinquième point et le réunir aux quatre autres est impossible sans croisement. Un pont est toujours nécessaire.

Voir Problème d'alimentation des trois maisons

Les cinq régions de De Morgan
En 1852, De Morgan prouvera proprement cette affirmation:	Il est impossible de disposer cinq régions de telle façon qu'il existe des frontières communes entre tous les couples possibles.

Voir Théorème de De Morgan

Bilan

L'impossibilité de réunir cinq régions complément mitoyennes entre elles ne prouvent pas le théorème des quatre couleurs (TQC) comme beaucoup l'on cru au XIX^e siècle.

Déductions faisables ou non

Si la carte 5-voisins existait, il faudrait cinq couleurs. VRAI.

Si la carte 5-voisins existait, alors le TQC est FAUX.

Si TQC est VRAI, alors il n'existe pas de carte 5-voisins. VRAI.

Mais …

Si la carte 5-voisins est FAUSSE, alors TQC est vrai: cette affirmation est FAUSSE.

Retour Suite	Historique – Quatre couleurs Diamant de Birkhoff Quatre couleurs – Index
Voir	Cinq pays Couleurs Démonstration Énigme des carrés mitoyens Graphe à 2 couleurs Indicateur d'Euler-Poincaré Introduction à la topologie Quadrichromie Ruban de Moebius Théorème des quatre couleurs Topologie – Glossaire Topologie – Index
DicoNombre	Nombre 4
Sites	Voir références
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Mobius.htm