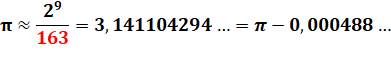|
Édition du: 09/05/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 70
/ 80 / 90
/ 100 / 110 / 120 / 130 / 140
/ 150 / 151 / 152 / 153 / 154
/ 155 / 156 / 157 / 158 / 159
/ 160 / 161 / 162 |
163 |
164 / 165 / 166
/ 167 / 168 / 169 / 170 / 171
/ 172 / 173 / 174 / 175 / 180
/ 185 / 190 / 195 / 200 / 250 / 300
/ 400 / 500 / 600 / 1000
/ Autres |
|
![]()
|
|
|
|
Suite en propriétés
arithmétiques |
|
|
Vrai en soi: 100 – 36 = 64 = 4 x 16 Vrai aussi en remplaçant classiquement les lettres par
des chiffres: 263² – 163² = 4 x 10 650. Seule
solution. |
Chiffres et numération
|
163 => 361 = 192 |
Liste: 23, 61, 163, 521, 691, 821, 1297, 1861,
4201, 4441, 4483, 5209, 5227, 9049, 9631, …
Liste: 61,
163, 487, … |
|
|
163 + 1×6×3 = 181 163 – (1+6+3) = 153 = T17 |
|
|
|
16310 = 11712 17112 = 22910 71112 = 102110 |
|
|
|
163 => 1² = 1, 6² = 36,
3² = 9
=> 1369 = 37² |
|
|
Multiplication, division, diviseurs
|
163 |
|
|
163 et 167 sont cousins. |
|
|
163 = 4 x 41 – 1 |
|
Avec les puissances
|
163 = 1 + 2 × 34 |
|
|
|
163 = 1² + 9² + 9² |
|
|
|
163 = 4² + 7² + 7² +
7² = 3² + 4² + 5² + 7² + 8² |
|
|
|
163
= 23 + 33 + 43 + 43 = 14 + 34
+ 34 |
|
|
En puissances
|
2, 4, 8 163, 26569, 4330747 1514, 2292196, 3470384744 28114, 790396996, 22221221145544 |
2, 4, 8 3, 9, 27 8, 64, 512 |
Dénombrement, jeux et curiosités
|
|
|
Autour du nombre
|
Écart 1,26
… 10-6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J.J.
Gould – 1972 Cité par
François Le Lionnais – Les
nombres remarquables |
|
|
|
|
–1,
–2, –3, –7, –11, –19, –43, –67, et –163 |
|
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
163 2,
[1, 0, 1, 0, 0, 0, 1, 1] 3,
[2, 0, 0, 0, 1] 4,
[2, 2, 0, 3] 5,
[1, 1, 2, 3] 6,
[4, 3, 1] 7,
[3, 2, 2] 8,
[2, 4, 3] 9,
[2, 0, 1] 10,
[1, 6, 3] 11,
[1, 3, 9] |
12,
[1, 1, 7] 13,
[12, 7] 14,
[11, 9] 15,
[10, 13] 16,
[10, 3] 17,
[9, 10] 18,
[9, 1] 19,
[8, 11] 20,
[8, 3] 21,
[7, 16] |
22,
[7, 9] 23,
[7, 2] 24,
[6, 19] 25,
[6, 13] 26,
[6, 7] 27,
[6, 1] 28,
[5, 23] 29,
[5, 18] 30,
[5, 13] 60,
[2, 43] |
Aucun |
Voir Bases / Brésiliens
![]()
|
Suite |
·
Nombre 164 |
|
Voir |
|
|
Cette page |
![]()