Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 05/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	60	61		62	63		64	65	66	67	68	69

Nombre 61

Maths 61

Culture 61

Numération 60 à 69

Soixante-et-un

Sixty-one

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	11 1101
Bases	1416
Romain	LX I

Suite

61 = 5² + 6²

Caractérisation du nombre

5 - bonacci

Binomial

Congruent

Déficient

Docile (amenable)

Fortuné

Impair

Lucas premier (rang)

Nombre de Keith

Nombre d'Euler (n°3)

Premier

Premier cubain

Premier de Pythagore

Premier faible

Premier inévitable (ou minimal)

Premier irrégulier d'Euler

Premier jumeau avec 59

Premier long

Premier minimal

Premier pointé

Premier régulier

Premier sexy

Sécant

Carré centré (6^e)

Hexagonal centré (5^e)

Décagonal centré (4^e)

Icosagonal centré

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

CARTE D'IDENTITÉ
Nombre	Premier	Département	Orne
Facteurs	61 = 1 x 61	Élément	PROMÉTHÉUM Pm
Ptés Typiques	61 = 5² + 6²	Mnémo	CHÂTEAU
	Suite Maths		Suite Culture

Propriétés CULTURELLES

Soixante-et-un

Soixante-et-unième

Voir Orthographe des nombres

Espagnol Italien	Anglais Allemand
Sesenta y uno Sessantuno	sixty-one einundsechzig

Voir Numération 60 à 69

Nombres et langues

Police

61 : Accident de la route provoqué par un tiers non identifié, selon le code de la police new-yorkaise.

>>>

---

Propriétés MATHÉMATIQUES

Chiffres et numération

61	N'est repdigit dans aucune base. Il n'est pas brésilien.
61 + 16 = 77 61 – 16 = 45 = T9		Devient repdigit lorsqu'ajouté à son retourné et triangulaire en le retirant.
61 + 6 × 1 = 67		Pointe vers le nombre premier suivant en lui ajoutant ses chiffres
6110 = 1655		Exactement les mêmes chiffres en base 55.
61 => 16 = 2^4		Premier dont le retourné est une puissance. Liste: 23, 61, 163, 521, 691, 821, 1297, 1861, 4201, 4441, 4483, 5209, 5227, 9049, 9631, …
61 => 6² = 36, 1² = 1 => 361 = 19²		Nombre dont les chiffres mis au carré puis concaténés produit un carré.
61 => 6 + 1 = 7, 1 + 7 = 8 puis: 15, 23, 38, 61		Keith et Fibodiv: Avec 6 et 1 comme premiers nombres, la somme du type Fibonacci crée une suite où le nombre est présent.
61 => 16 = 4² 96 979 => 97 969 = 313² 123 373 => 373 321= 611²		Nombres premiers dont le retourné est un carré Voir Nombres à motifs

Addition et soustraction

61 = 2 + 4 + 8 + 16 + 31

5 - bonacci.

Multiplication, division, diviseurs

61 = 1 x 61	Premier, jumeaux avec 59.
61 = 6 x 10 + 1 = 5 (4² – 4) + 1	Nombre hexagonal centré. Nombre décagonal centré.
	Division avec des factorielles.
6, 1, 7, 8, 15, 23, 38, 61	Nombre de Keith, premier.
k | (n^3 + 3) & (n + 1)^3 + 3 alors k = 61	Si un nombre divise à la fois ces deux expressions, alors ce nombre est 61. Exemples ci-dessous.

Exemples

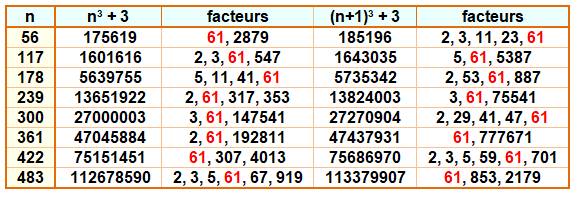
Voir Nombre 5 pour autres exemples

61 = 61 1 facteur 62 = 2 x 31 2 facteurs 63 = 3² x 7 3 facteurs	Trois nombres consécutifs dont la quantité de facteurs va croissant de 1 à 3 Voir Nombre 661
61 = 61 62 = 2 x 31	Plus petite suite de deux nombres dont le plus grand facteur se termine par 1.
61 = 6 469 693 291 – 6 469 693 230 61 = 7 420 738 134 871 – 7 420 738 134 810		Nombre fortuné: différence entre primorielle et le premier juste plus grand (d'au moins 2).
	Plus petite succession de quatre "tau" croissants. Tau est la quantité de diviseurs de n. Liste: 61, 193, 277, 361, 397, 421, 457, 613, 757, 997. Voir Nombre 11 371
	Premier cas en OMÉGA croissant. OMÉGA est la quantité de facteurs répétés.

Avec les puissances

61 = 5² + 6² = 25 + 36 = 3² + 4² + 6² = 9 + 16 + 36	Nombre binomial. Somme des carrés de nombres consécutifs. Nombre carré centré. Les deux seules sommes à deus ou trois termes.
61 = 2² + 2² + 2² + 7² = 2² + 4² + 4² + 5²	Somme des carrés de quatre nombres premiers. Seule autre somme de quatre termes.
61 = 31² – 30² = 31 + 30	Motif général pour tout nombre impair.
61 = 5^3 – 4^3= 125 – 64	Nombre binomial. Premier, différence de deux cubes successifs; tous de la forme 6k + 1. Forme générique: ( y^3 – x^3 ) / (y – x) avec y = x + 1

En puissance

61² = 60² + 11² = 3600 + 121 = 3721

9^e triplet de Pythagore primitif. 5^e avec hypoténuse = côté – 1.

Autour du nombre

Nombre premier long. La période du développement décimal de la fraction est maximale en une seule suite permutée pour toutes les fractions avec ce dénominateur.
63! – 61! = 63 x 62 x 61! – 61! = (63 x 62 – 1) 61! = 3 905 x 61! = 5 x 11 x 71 x 61! = k . 61!	Exemple de calcul de la somme ou de la différence de deux factorielles.
1 318 820 881 ² = 173 928 851 61 61 61 61 61 508 853 989 ² = 25 893 238 21 21 21 21 21	Si un carré se termine par xy xy xy xy xy alors xy = 21, 61 ou 64.

Jeux, combinatoire et curiosités

		Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5
	Comment écrire 61 avec des puissances de 3.
61 = Qe(6)	Quantité de permutations d'Euler avec 6 termes.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 1, 0, 1] 3, [2, 0, 2, 1] 4, [3, 3, 1] 5, [2, 2, 1] 6, [1, 4, 1] 7, [1, 1, 5] 8, [7, 5] 9, [6, 7] 10, [6, 1] 11, [5, 6]	12, [5, 1] 13, [4, 9] 14, [4, 5] 15, [4, 1] 16, [3, 13] 17, [3, 10] 18, [3, 7] 19, [3, 4] 20, [3, 1] 21, [2, 19]	22, [2, 17] 23, [2, 15] 24, [2, 13] 25, [2, 11] 26, [2, 9] 27, [2, 7] 28, [2, 5] 29, [2, 3] 30, [2, 1] 60, [1, 1]	60, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 62 Voir en haut de page DicoNombre
Voir	Abaque Romain Code Gray Croissance Logistique Échec Multiplications Védiques Produit Palindrome Satellites
Cette page	http://villemin.gerard.free.fr/NombDico/Nb50a100/Nb61.htm