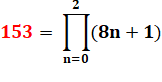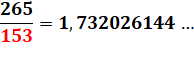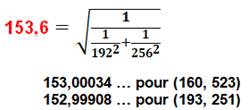|
Édition du: 29/04/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 70
/ 80 / 90
/ 100 / 110 / 120 / 130 / 135
/ 140 / 141 / 142 / 143 / 144
/ 145 / 146 / 147 / 148
/ 149 / 150 / 151 / 152 |
153 |
154 / 155 / 156
/ 157 / 158 / 159 / 160 / 161
/ 162 / 163 / 164 / 165 / 170
/ 180 / 190 / 200 / 250 / 300
/ 400 / 500 / 1000 / Autres |
|
![]()
|
|
|
||
|
Suite en propriétés
arithmétiques |
|
|
|
|
153
= 1 + 125 + 27 = 1 + 2 + 6 + 24 + 120
Voir
Brève 689 avec calculs / Démonstration |
|||
|
|
||
|
Selon Évagre le Pontique (346-399, moine
vivant dans le désert d'Égypte): |
||
|
|
||
|
Maths |
|
![]()
Chiffres et numération
|
153 = 100110012 = 21214 = 9916 |
|
|
|
153 =
17 (1 + 5 + 3) |
|
|
|
153 =
3 x 51 |
|
|
|
153 + 360 = 513 |
||
|
153
– (1 + 5 + 3) = 144 = 12² |
|
|
|
153 et 351 |
|
|
|
153
+ 351 = 504 504² = 288 x 882 |
|
|
|
153 + 315 + 531 = 999 351 + 135 + 513 = 999 |
|
|
|
|
|
|
Addition et soustraction
|
153 => 54 770 336 324 dont 77 avec 1 et 2 |
|
|
153 = 1 + 111 + 5 + 3
+ 33 |
|
|
153
= 1 + 2 + 3 + 4 +…+ 17 = ½ x 17 x 18 |
à composante triangulaires: 15 et 3.
|
|
153 = 1! + 2! + 3! + 4! + 5! |
|
|
153 = 1 + 2 + 3 + 7 + 11 + 19 + 43 + 67 |
|
Multiplication, division, diviseurs
|
153 =
32 x 17 |
|
|
|
|
|
153 = 3² x 17 => 3 + 17 = 20 |
|
|
Div(153) => 1+3+9+17+51 = 81 = 9² Div(231)
=> 1+3+7+11+21+33+77 = 153 |
|
|
|
Somme
Div(153) = 1+3+9+17+51+153 = 234 Somme
DivPropre(153) = 1+3+9+17+51 = 9² Produit
DivPropre(153) =1x3x9x17x51 = 23409 |
|
|
|
|
|
|
Avec les puissances
|
153
= 13 + 53 + 33 |
|
|
|
1 + 5 + 3 =
9 = 3² 1 x 5 x 3 =
10 + 51 + 32 = 15 12 + 52
+ 32 = 35 |
|
|
|
153 ⇦ |
|
|
|
153 = 23 + 33 + 33 + 33 + 43 |
|
|
153 =
3² + 12² = 2² + 7² + 10² = 4² + 4² + 11² = 5² + 8² + 8² = 6² + 6² + 9² |
|
|
153 = 77² – 76² |
|
![]()
En puissance
|
2153
= 11 417 981 541
647 679 048 466 287 755 595 961 091 061 972 992 |
|
Dénombrement, jeux et curiosités
|
|
|
|
|
Notez comme il est plus facile de calculer (18, 2) plutôt que (18, 16) = (18x17x16x…x3) / 16! |
Carré magique sept-segment
Reste magique en le retournant avec la somme 177
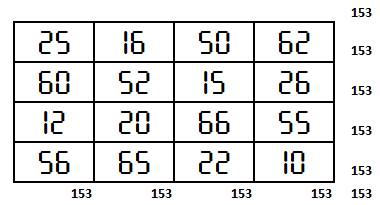
Voir Carré magique
réversibles
Autour du nombre
|
|
|
|
115153 => premier |
|
|
153 153 |
|
Décimales
|
153,27
= 666 – 512,73 |
|
|
|
Doublets se rapprochant de la valeur entière 153.
Le premier tient le record pour les nombres de 1 à 1000; alors que le second
est le plus proche de (192, 256). |
![]()
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
153 2, [1, 0, 0, 1, 1, 0, 0, 1] 3,
[1, 2, 2, 0, 0] 4, [2, 1, 2, 1] 5,
[1, 1, 0, 3] 6,
[4, 1, 3] 7,
[3, 0, 6] 8, [2, 3, 1] 9,
[1, 8, 0] 10,
[1, 5, 3] 11,
[1, 2, 10] |
12,
[1, 0, 9] 13, [11, 10] 14,
[10, 13] 15,
[10, 3] 16, [9, 9] 17,
[9, 0] 18,
[8, 9] 19,
[8, 1] 20,
[7, 13] 21,
[7, 6] |
22,
[6, 21] 23,
[6, 15] 24,
[6, 9] 25,
[6, 3] 26,
[5, 23] 27,
[5, 18] 28,
[5, 13] 29,
[5, 8] 30,
[5, 3] 60,
[2, 33] |
16,
[9, 9] 50,
[3, 3] 152,
[1, 1] |
Voir Bases / Brésiliens
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()