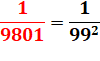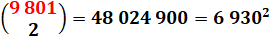NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/04/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres		DicoNombre NOMBRES								Glossaire Nombres
1 10 100 1000 5000 6000 7 000 8000		9 000 à 9 999								10 000 15 000 20 000 50 000 100 000 10^6 10^9 10^100
		Neuf mille Anglais: Nine thousand
9 000	9 100		9 200	9 300	9 400	9 500	9 600	9 800	9 900		9 900

9 000

9 000 = 2^3 x 3^2 x 5^3 = 9 × 100	Facteurs
9 000 = 10^3 + 11^3 + 12^3 + 13^3 + 14^3 = 1 000 + 1 331 + 1 728 + 2 197 + 2 744		Somme de cinq nombres successifs portés à une puissance (ici: 3). Toutes ces sommes sont divisibles par 5, sauf pour les puissances en multiple de 4.
9 001	Premier minimal.
9 010² = 25² + 26² + … + 624² = 81 180 100	Somme d'entiers consécutifs = carré.
9 024² = 81 432 576	Tous les chiffres de 1 à 8.
9023 … 14567	Parmi les nombres à quatre chiffres, c'est le nombre 9023 qui est le plus éloigné du nombre suivant à chiffres distincts sans retrouver les chiffres de 9023. Les neuf chiffres sont différents.
9 077	Nombre de Markov.
9 091 car 9 091 x 11 = 100001	Ce nombre, comme11, divisent les nombres en abcdeabcde = 10001 x abcde = 9091 x 11 abcde Exemples: 1 234 512 345 / 9 091 = 135 795 9 876 598 765 / 9 091 = 1 086 415
9 197 = 42² + 53² + 68² = 24² + 35² + 86²			Égalité palindromique trouvée par Benjamin Vitale

1 296 = 36^2 = 6^4 2 916 = 54^2 9 216 = 96^2 9 261 = 21^3	Motif avec permutation des chiffres sur trois nombre, assez rare.
9 216 = 96² × 1 2 916 = (9 × 6)² x 1	Opération avec ses chiffres. Curiosité avec les mêmes chiffres.
9 216 = 104² – 40² = 96² = 12² x 8² 9 216 = 146² – 110² = 96² = 16² x 6² 9 216 = 296² – 280² = 96² = 24² x 4²	Nombre complètement carré.
9 713 × 2 468 = 23 971 684 9 713 × 2 846 = 27 643 198	Nombres de Friedman: tous les chiffres sauf le 5 sont de chaque côté du signe égal.
9 232	Maximun du cycle de Collatz pour le nombre 27.
9 240 = 20x21x22 = 3 x 55x56	Voir Nombre à la fois triangulaires et tétraédrique.
9 240 & 7 560	Ces deux nombres ont 63 diviseurs chacun, maximum pour les nombres à 4 chiffres ou moins.
9 049	Premier minimal.
9 261 = 185^2 – 158^2 = 7^3 × 3^3 = 21^3	Différence de carré = produit de cubes.
9 376² = 87 909 376 109 376² = 11 963 109 376	Nombre automorphique à quatre chiffres. Le suivant à six chiffres.
… 9376^k = … 376	Toutes les puissances des nombres en …9376 se terminent par 9376.

Cinéma	HAL 9000: nom du superordinateur qui se rebelle dans le roman d'Arthur Clark et dans le film 2001 l'Odyssée de l'espace de Stanley Kubrick (1968).
Normes	ISO 9000 ensemble de normes relatives à la gestion de la qualité publiées par l'Organisation internationale de normalisation (ISO). ISO 9001 Fixe les exigences de qualité d'une société fortement orientée conception. ISO 9002 Idem pour les sociétés plutôt orientées vers la fabrication, la production ou alors les prestations de service. ISO 9003 S'applique aux sociétés réalisant des contrôles et des essais.
Jeux	9 036 briques pour le Colisée de Rome par Lego^TM Record pour cette boite de jeux proposée pour Noël 2020. Lego a été créé en 1949 par Ole Kirk Christiansen, un charpentier danois de Billund qui utilisait des chutes de bois pour fabriquer des jouets. Son entreprise se nomme "leg godt" en danois qui veut dire "joue bien". Suite: Et Lego créa la brique – Le Figaro – Laure Kermanac'h – 11/12/2020

9 400

Mnémo

9 401 correspond aux lettres BRST comme celles de Brest.

>>>

9 474 = 9^4 + 4^4 + 7^4 + 4^4 = 6 561 + 256 + 2401 + 256

Nombre narcissique Voir Motifs / Table des nombres de Keith

9 500

9 603^3 = 14^3 + 19^3 9 604^3 = 7^3 + 21^3	Somme de deux cubes pour deux nombres successifs. Voir Nombre 854
4 096 = 64^2 9 604 = 98^2	Motif avec permutation des chiffres.
9 642 × 87 531 = 843 973 902	Multiplication pannumérique (tous les chiffres) donnant le plus grand produit. Pour obtenir ce résultat: Commencer avec les plus grands chiffres. Maintenez les deux nombres aussi proches que possible. Le but est de réaliser un rectangle proche d'un carré (À périmètre constant, l'aire est maximale avec le carré).
9 649	Premier minimal.
		Expression approchant un nombre entier. Avec 5, curiosité avec nombre proche de 1000 et avec répétition de 666.

9 702 = 98 x 99 = 98² + 98 = 54² + 56² + 59² + 54 +56 +59 = 54×55 + 56×57 + 59 ×60	Quadruplet complémenté amusant.
9 73010 = 3 79014	Exactement les mêmes chiffres en base 8. Vrai pour tous les nombres de la dizaine. Propriété: 3x14^3 + 7x14^2 + 9x14 = 9730
9 768 = 264 × 37	Chiffres décroissants, multiple de 37.
9 788 9 + 7 = 8 + 8	Plus grand nombre équilibré non banal à quatre chiffres. Les précédents: …, 9568, 9577, 9586, 9678, 9687.
9 789! = 2,65019 ... 10^34 816	Factorielle 9 789 compte 34 817 chiffres et parmi eux, on retrouve le nombre 9 789, onze fois. C'est le plus petit cas pour onze fois. C'est la répétition maximale pour un nombre à quatre chiffres.
9 797 = 97 × 101 77 = 7 × 11	Formés de deux fois le même nombre et produit de deux nombres premiers consécutifs (rare).
	Nombre greffe: deux seuls nombres à quatre chiffres tels que le nombre est présent dans sa racine carrée, juste après la virgule. Voir 77

Nombres dont la racine carrée reprend le nombre après la virgule

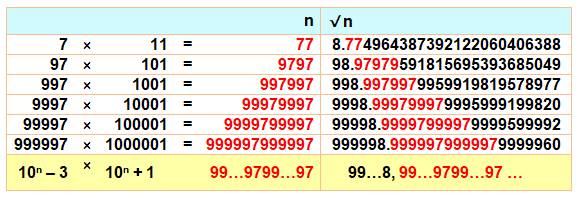
Si pas forcément après la virgule, on a:

Liste: 0, 1, 8, 77, 98, 99, 100, 764, 765, 5711, 5736, 9797, 9998, 9999,

10000, 76394, 77327, 997997, 999998, 999999,

1000000, 2798254, 7639321, 8053139, 25225733,

Voir Nombre greffe / OEIS A232087 – Grafting numbers.

Curiosité rare avec les décimales des racines carrées

9 800

9 800 = 2^3.5^2.7^2 9 801 = 3^4.11^2	Nombres puissants jumeaux (couple n°4).
98 00 = 99² – 1 = (100 – 1)² – 1	Motif en 98 et 99 avec application du développement du carré. Le carré d'un repdigit de k "9" moins 1 est égal à un nombres de k – 1 fois "9" , suivi d'un "8" et suivi de k fois "0".

9 801 = 99² = 11² × 9² = 11² × 3^4 1 089 = 99² / 9	Nombre et son retourné en 9. Objet d'un motif itératif.
9 801 = 99² & 99 = 98 + 01	Nombre de Kaprekar.
	Tous les nombres jusqu'à 99, sauf 98. Voir Nombre de Lewis Carroll
9 801 = 99^2 1 089 = 33^2	Motif avec permutation des chiffres. Les racines sont dans un rapport 3. Voir Nombre et son retourné 1089
8 712 = 2 178 × 4 9 801 = 1 089 × 9	Nombre divisible par son retourné. Ils ne sont que deux et engendrent une famille infinie.
9 801 = 101² – 20² = 99² = 11² x 9² 9 801 = 549² – 540² = 99² = 33² x 3²	Nombre complètement carré.
1000 / 9801 = 0,01020304_979900 0102 … (trait = tous les nombres de 04 à 97)	Fraction qui engendre tous les nombres jusqu'à 99, en omettant le 98. Période de 196 chiffres.
	Cas rare où le coefficient du binôme est une puissance.
9 802 – 1 = 99² 9 802/2 – 1 = 70²	Nombre et sa moitié produisant des carrés.
98029801 = 9901²	Nombre de Sastry: devient carré en concaténant son successeur.

9 867 = 11 × 897	Plus grand nombre à quatre chiffres différents divisible par 11.
9 872 = 8 + 88 + 888 + 8888	Somme des nombres en 8.
9876 est divisible par 4 987 est divisible par 3 98 est divisible par 2 9 est divisible par 1	Nombre polydivisible: le plus grand à quatre chiffres.
9 899 = 100² – 100 – 1	Opération avec chiffres 0 et 1.
	Nombre de Fibonacci inverse (le deuxième). Contient la séquence de Fibonacci avec les premiers nombres en clair jusqu'à 55, les suivants sont enfouis du fait de la propagation des retenues. L : longueur de la période de la fraction.

9 900

9 950^1/3 = 21,50837964…	Les dix premiers chiffres sont pannumériques.
9 944 = 10 033 496 / 82	Avec 10 033 496 = somme des facteurs les plus grands jusqu'à 9 944.
9 949	Premier minimal.
9 963 = 9^3 + 9^3 + 6^5 + 3^6 = 729 + 729 + 7776 + 729	Somme de ses chiffres en puissances. Plus grand à quatre chiffres.
9 990 = 37 x 270 = 111 x 90 = 333 x 30 = 666 x 15 = 999 x 10	Divisible par 37 et autres.
9 999 = 3² × 11 × 101 = 9 × 1111	Code d’anomalie ou infini ou date inconnue pour les programmeurs. Attention à la date: 9/9/99.
	Curiosité rare avec les décimales des racines carrées
etc.	Tous les repunits avec 2k fois le "9" ont une racine carrée qui commence avec 2k fois le "9".
9999² = 9 998 0001 9999 = 9998 + 0001 9999^3 = 9997 0002 9999 9999 x 2 = 9997 + 0002 + 9999 9999^4 = 9996 0005 9996 0001 9999 x 2 = 9996 + 0005 + 9996 + 0001	Nombre de Kaprekar. Cette propriété est valable pour tous les repdigits en 9. Suite en Repdigits en 999 …
9999^3 = 999700029999	Production de 9; motif itératif.

Suite	Nombres 10 000
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N9000.htm

Quelques repères dans ces pages

>>> Nombre 9 240 DIVISEURS

>>> Nombre 9 474 NARCISSIQUE

>>> Nombre 9 642 PANNUMÉRIQUE

>>> Nombre 9 801 KAPREKAR

>>> Nombre 9 999 CURIOSITÉS