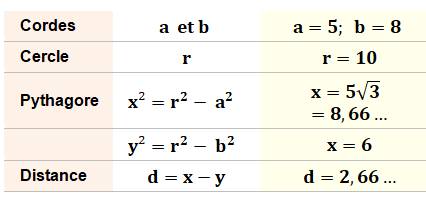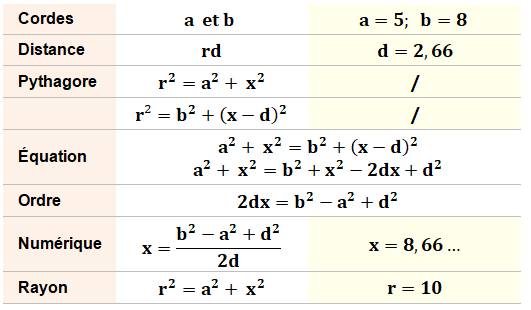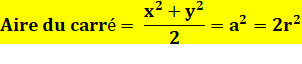|
Édition du: 09/07/2022 |
|
INDEX |
CERCLE – Propriétés |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Cordes parallèles Deux cordes
parallèles sur un cercle. On connait leur longueur Trouver l'écart
entre elles connaissant le rayon du cercle. Simple! Trouver le
rayon, connaissant l'écart. Pas plus difficile. |
||
|
|
Sommaire de cette page >>> Cordes parallèles >>> Calcul de la distance d >>> Calcul du rayon r >>> Cercle et carré inscrit |
Débutants Glossaire |
|
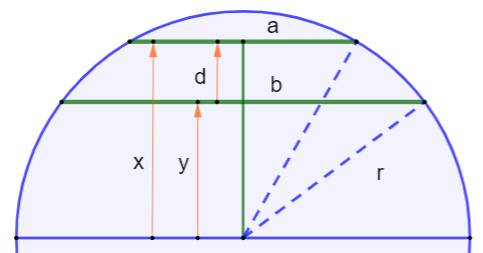
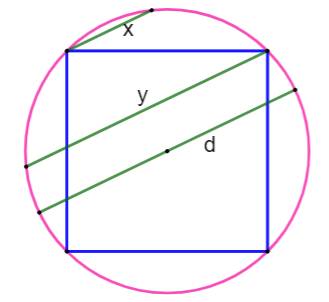
Construction et notations Un cercle de rayon r et deux cordes parallèles de
longueur 2a et 2b. Les distances au diamètre parallèle sont x et y. La distance entre les cordes et notée d. On connait a, b et r calculer d. On connait a, b et d, calculer r. |
|
|
|
Calculs On donne a, b et r. Les distances se calculent en invoquant le théorème
de Pythagore. |
|
|
|
Calculs Même principe que ci-dessus. Une expression en x² qui, par bonheur, se réduit
en une expression du premier degré. |
|
|
|
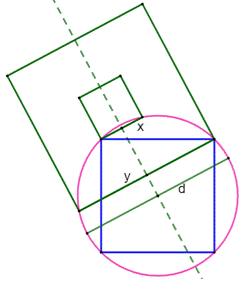
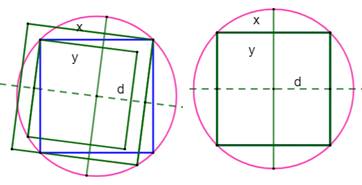
Construction Un carré inscrit dans le cercle. Un diamètre quelconque. Deux cordes parallèles à ce diamètre et issues
des sommets du carré. Propriété
Avec a le côté du carré et r le rayon du cercle. |
|
|
|
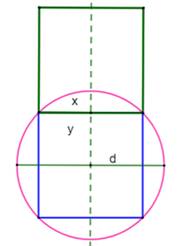
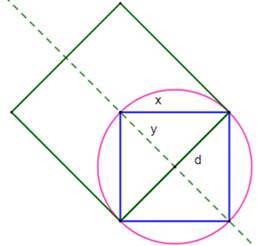
Autrement-dit L'aire du carré inscrit (bleu) est égale à la demi-somme
des aires des carrés verts, construits sur les cordes. Cela est vérifiable pour les cas particuliers (voir ci-dessous)
|
|
|
|
|
||
![]()