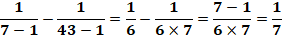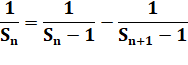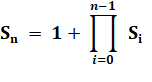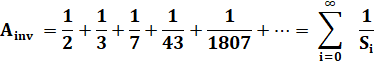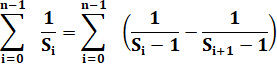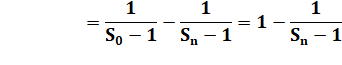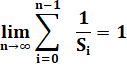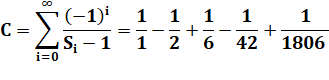Suite de Sylvester

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/12/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Général	Construction particulière					Glossaire Général
INDEX Nombres (Classification)	Ulam	Chanceux d'Ulam		Mian-Chowla	Sylvester
		Hofstadter–Conway		Suites équilibrées	Dedekind
			Sommaire de cette page >>> Caractéristiques de la suite >>> Termes de la suite de Sylvester >>> La somme des inverses est convergente >>> Programmation

Suite de SYLVESTER – Caractéristiques
Famille	Nombre / Produit / Itération
Définition	Nommés aussi nombres d'Euclide La suite de Sylvester est définie par le produit de tous les termes précédents plus 1.
Les premiers	1 (souvent considéré comme non appartenant à la suite) 1 + 1 = 2 (est souvent noté comme s₀ ) 1 x 2 + 1 = 3 1 x 2 x 3 + 1 = 7 1 x 2 x 3 x 7 + 1 = 43 1 x 2 x 3 x 7 x 43 + 1 = 1 807 3 263 443 10 650 056 950 807 113 423 713 055 421 844 361 000 443 …
Récurrence	7 = 3 x 2 + 1 = 3 ( 3 – 1) + 1 43 = 7 x 6 + 1 = 7 ( 7 – 1) + 1 1 807 = 43 x 42 + 1 = 13 (43 – 1) + 1
Relation à noter
Construction
Propriétés	Croissance en exponentielle double: l'exposant de l'exponentielle est lui-même une exponentielle. E = 1,264084735306… la constante de Vardi La somme des inverses converge vers 1 et cela plus vite que toute autre suite. La décomposition en facteurs premiers n'est connue que pour les premiers termes. (Voir le tableau ci-dessous) Tous les nombres connus de la suite de Sylvester sont sans facteur carré. On ne sait pas si c'est toujours le cas. Les nombres de la suite sont mutuellement premiers entre eux. Cette suite peut être utilisée pour prouver qu’il existe une infinité de nombres premiers, car tout nombre premier peut diviser au plus un nombre dans la suite. Mieux, aucun facteur premier d'un nombre dans la séquence ne peut être congru à 5 modulo 6, et la suite peut être utilisée pour prouver qu'il existe une infinité de nombres premiers congrus à 7 modulo 12. La somme réduite (celle de la preuve par 9) des termes de la suite de Sylvester est égale à 7. Ex: 1807 => 1 + 8 + 0 + 7 => 9 + 7 => 7. Voir vérification par programme. Preuve par récurrence possible.
Historique	Vers 1880, James Sylvester (1814-1897) étudie les propriétés de cette suite.
Anglais	Sylvester's sequence is an integer sequence (S_i) where S₀ is 2, and S=i is one plus the product of all i previous terms: S_i = S₀ S₁ …S_i + 1. The sequence begins 2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443. The empty product of no terms is 1, so S₀ = 1 + 1 = 2 is a natural start.

Termes de la suite de Sylvester

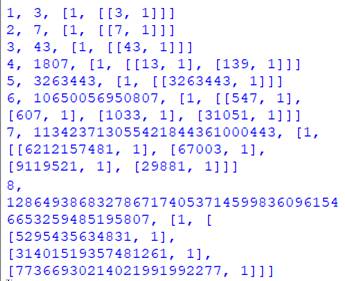
Les quatre premiers termes (2, 3, 7 et 43) sont premiers.

La numérotation commence avec a(0) = 2;

Ainsi a(4) = 1 807 = 13 x 139.

P68 = nombre premier de 68 chiffres; C416 = nombre composé de 416 chiffres

Les 44 chiffres du facteur de S₁₀ a été trouvé par Ken Takusagawa.

On connait le statut des nombres jusqu'à S₂₉ et au moins un des facteurs.

Suite de cette table sur la page de Jens Kruse Andersen.

La somme des inverses est convergente
Propriété	La somme des inverses de la suite de Sylvester tend vers 1. Voir Fractions égyptiennes (fraction avec numérateur unité)
Somme des inverses
Avec la relation vue ci-dessus et pour n termes
Un terme chassant le suivant et S₀ = 2
Pour n tendant vers l'infini
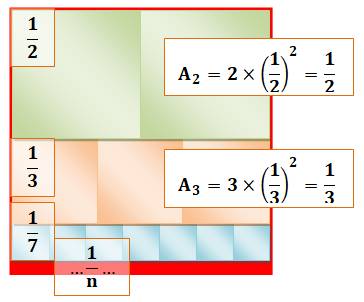
Visualisation de la somme des inverses de la suite de Sylvester Chaque carré à la dimension de 1/n. Son aire est donc (1/n)² et étant en quantité n, l'aire d'une bande est égale à 1/n. En rouge, les bandes suivantes non représentées car trop petites. L'ensemble des bandes couvre un carré de côté unité.
Constante de Cahen		Eugène Cahen a proposé cette série et prouvé que la constante est irrationnelle.

Anglais : sum of reciporcal of Sylvester sequence

Programmation (Maple)
Programme donnant S_n et sa factorisation	Commentaires Mise au propre au démarrage avec restart. La suite s commence par 2 et cette valeur est placée dans la liste L. Boucle pour le calcul des huit premiers nombres de la suite. On place la quantité de terme de la suite L dans q (nops = number of operands). Calcul du terme suivant de la suite avec une séquence en mul qui prend chaque terme de rang i pour i de 1 à q et les multiplie. La liste est mise à jour en y incluant le nouveau terme calculé. Demande d'impression (lprint) du rand n, du nombre de Sylvester s et de la factorisation de ce terme. Résultats Pour huit termes, la réponse (en bleu) est immédiate. Le calcul du neuvième exige une belle machine. Les valeurs du tableau ci-dessus sont extraites des tableaux trouvés sur Internet.
Programme donnant S_n et la somme des chiffres	Commentaires Même programme que ci-dessus jusqu'à la sixième ligne. Dans S, on place la conversion décimale du nombre S de Sylvester. Cette opération a pour effet de donner la liste de tous les chiffres de S. La quantité de chiffres et mémorisée en qS. Les chiffres S[i] sont additionnés pour i de 1 à qS. On calcule le reste de la division par 9 er C7 Impression avec lprint. Résultats À l'exception des deux premiers nombres de la suite (2 et 3), la somme réduite des nombres de Sylvester est égale à 7.

Voir Programmation – Index

Suite	Nombres chanceux d'Ulam Nombre chanceux d'Euler Nombre chanceux par plage
Voir	Crible d'Ératosthène
DicoNombre	Nombre 1,2640… Nombre 7 Nombre 43 Nombre 1 807 Nombre 3 262 443
Sites	Suite de Sylvester – Wikipédia Sylvester's sequence – Wolfram MathWorld OEIS A000058 – Sylvester's sequence: a(n+1) = a(n)^2 - a(n) + 1, with a(0) = 2 Factorization of Sylvester's sequence – Jens Kruse Andersen – 2012
Cette page	http://villemin.gerard.free.fr/aNombre/TYPSEQUE/Sylveste.htm