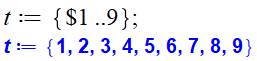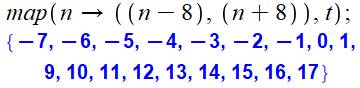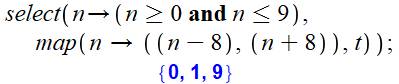|
||||||||||||||||||||||||||||||||
![]()
|
NOMBRES ORPHELINS ou avec antécédents Définition: On
nomme antécédent (soustractif) d'un
nombre, un nombre tel que les différences absolues des chiffres consécutifs
de celui-ci produisent le nombre.
|
Anglais: numbers such that no digit is exceeded by the digit to
its left
|
|
|||||||
|
Exemple 123 Le nombre
123 possède 46 "pères" ou antécédents,
y compris deux commençant par un 0. Par
exemple 5425 devient:
|
123, 0130 123, 0136 123, 1025 123, 1203 123, 1241 123, 1247 123, 2130 123, 2136 123, 2314 123, 2352 123, 2358 123, 3203 123, 3241 123, 3247 123, 3425 123, 3463 |
123, 3469 123, 4314 123, 4352 123, 4358 123, 4530 123, 4536 123, 4574 123, 5425 123, 5463 123, 5469 123, 5641 123, 5647 123, 5685 123, 6530 123, 6536 |
123, 6574 123, 6752 123, 6758 123, 6796 123, 7641 123, 7647 123, 7685 123, 7863 123, 7869 123, 8752 123, 8758 123, 8796 123, 8974 123, 9863 123, 9869 |
||||
|
Quantité d'antécédents pour les
nombres de 100 à 125. C'est le nombre 111 qui tient le record jusqu'à
1000 avec 64 ascendants. |
[100, 18], [101, 34],
[102, 30], [103, 26], [104, 22], [105, 18], [106, 14], [107, 10], [108, 6],
[109, 2], [110, 34], [111, 64], [112, 58],
[113, 50], [114, 42], [115, 34], [116, 26], [117, 18], [118, 10], [119, 4],
[120, 30], [121, 56], [122, 52], [123, 46], [124, 38], [125, 30] |
||||||
|
Antécédents de 111 Ce sont
les 64 nombres à trois quatre chiffres dont chaque chiffres et égal à son
voisin à un près. Dont
trois avec un 0 en tête. Le nombre
11 possède 34 antécédents. |
0101 0121 0123 1010 1012 1210 1212 1232 1234 2101 2121 2123 2321 2323 2343 2345 |
3210 3212 3232 3234 3432 3434 3454 3456 4321 4323 4343 4345 4543 4545 4565 4567 |
5432 5434 5454 5456 5654 5656 5676 5678 6543 6545 6565 6567 6765 6767 6787 6789 |
7654 7656 7676 7678 7876 7878 7898 8765 8767 8787 8789 8987 8989 9876 9878 9898 |
|||
|
|
|||||||||||||
|
Autant
pour certains nombres, il existe de multiples antécédents, autant il existe
quantité d'orphelins. Le plus
petit est le nombre 648,
suivi de 649. Le nombre
109 n'a que deux antécédents. |
Liste 47 des orphelins à trois chiffres 648, 649, 659, 737, 738, 739, 747, 748, 749, 758,
759, 769, 828, 829, 837, 838, 839, 846, 847, 848,
849, 857, 858, 859, 868, 869, 879, 919, 928, 929, 937, 938, 939, 946, 947,
948, 949, 956, 957, 958, 959, 967, 968, 969, 978, 979, 989, … Notez que le retourné d'un orphelin est aussi un orphelin
(648 et 846). |
||||||||||||
|
Inversement:
tout nombre supérieur à 9 possède un fils formé par la concaténation des
différences absolues entre ses chiffres consécutifs. Tout père
à un fils: tout nombre à un successeur. Un fils
peut avoir aucun père (orphelin) ou de multiples pères (antécédents). |
Exemples
|
||||||||||||
Voir Brève
592
|
|
||
|
Pour les
nombres n de 0 à 9 |
Antécédents avec les nombres à deux chiffres distants de n. Exemple
pour 5, on a: 16, 27, …72, 61 … |
|
|
Pour les
nombres n à deux chiffres, les antécédents sont nombreux. Ils sont 18
pour le nombre 10 et 34 pour le nombre 11, le record pour deux chiffres. |
Antécédents de 10: 100, 122,
211, 233, …877, 899, 988. Antécédents de 11: 101, 121,
123, 210 …898, 987, 989. |
|
|
|
||
|
Nombres à
quatre chiffres. Record
d'antécédents pour 1111. Minimum
de deux antécédents pour 1009. Plus
petit orphelin à quatre chiffres pour 1648. |
18 antécédents de 1000: 10000, 12222,
21111, 23333 … 87777, 89999, 98888. 122 antécédents de 1000: 10101,
10121, 10123, … 45678, 54321 … 76543,
98789, 98987, 98989. |
|
|
Construction des orphelins |
Si n est un nombre orphelin, alors tous les nombres qui commencent ou
finissent par ce nombre sont orphelins. De même que tous ceux obtenus par insertion de 0. |
|
Voir Table des nombres orphelins jusqu'à 10 000
|
|
||
|
Principe La recherche des nombres orphelins se prête à un exercice de
programmation où l'utilisation astucieuse des ressources d'un logiciel permet
de raccourcir grandement le programme. Mais, cela nécessite une explication pas à pas de l'effet de ces
instructions. |
||
|
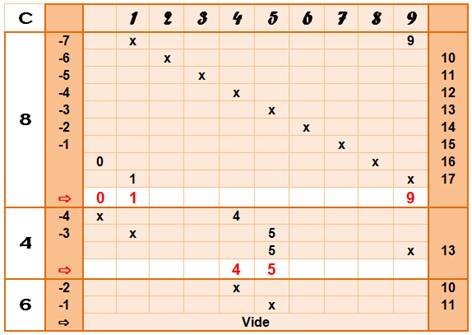
Tableau de recherche des antécédents de 648
|
Algorithme de recherche: exemple avec
648 En fait, on va chercher la possibilité d'un
antécédent. Avec le chiffre 8, pour tous les
nombres de 1 à 9, il faut chercher les possibilités d'avoir un chiffre
antécédent éloigné de 8. Objet des lignes sous C = 8 dans le tableau. En
éliminant tous ceux qui sortent de la fenêtre de 0 à 9, il ne reste que 0, 1
et 9. Avec le chiffre 4, il faut
chercher les possibilités avec les chiffres qui restent possibles (0, 1 et 9)
et une distance de 4. Seul 4 et 5 subsistent. Avec le chiffre 6, il faut une distance
6 et, les nouveaux nombres possibles sortent de la zone 0 à 9. Bilan: il n'y pas de
possibilité d'antécédent pour 648. |
|
|
Création de la liste initiale des chiffres
possibles
|
Le symbole $1..9 crée la suite des nombres de 1 à
9. Les accolades créent un ensemble,
qui est une liste sans répétition. |
|
|
Création de la première sélection avec 8
|
Cette instruction (map)
demande que l'opération indiquée soit exécuté sur tous les éléments de
l'ensemble t. L'opération est double: soustraire 8 et ajoutez 8
à chacun des éléments. |
|
|
Conservation des nombres dans le
bon intervalle
|
Extraction des nombres dans la fourchette (0, 9)
avec select. D'abord la condition de tri (n entre 0 et 9
compris), puis l'opération map vue
ci-dessus. |
|
|
Programme complet
|
La recherche des antécédents fait l'objet d'une
procédure (orph). Le nombre n
est converti en base 10 de manière à disposer des chiffres isolés dans la
liste L. Création de l'ensemble initial des chiffres en t. Boucle pour analyser les chiffres successifs de n. Opération de recherche telle qu'expliquée
ci-dessus. Si l'ensemble final est vide, comme pour 648,
retourner la variable vraie (true). Le programme principal utilise à nouveau
l'instruction selet pour ne garder, parmi les nombres de 100 à
800, que ceux pour lesquels orph est
vraie. |
Voir Programmation – Index
Programme original de Robert Israel
(OEIS A271639)
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()