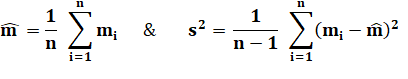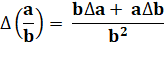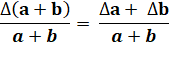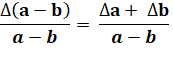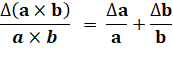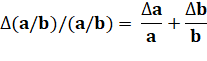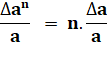NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/12/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	NOMBRES
Débutants Nombres	En représentation			Glossaire Nombres
INDEX Numération	Décimal	Bloc de trois	Arrondi	Virgule flottante
		Présentation	Incertitude	Ordre de grandeur
			Résolution
		Sommaire de cette page >>> Vocabulaire >>> Mesure – Exemple >>> Demi-unité du dernier chiffre exprimé >>> Paramètres associés à une mesure >>> Quelques remarques d'écriture >>> Précision et justesse

Résultats de mesure

INCERTITUDE et PRÉCISION

Les nombres décimaux comportent des chiffres derrière la virgule. Combien? Que signifient-ils?

Voyons, d'abord le cas d'un nombre seul, sans autre indications >>>

Puis, indiquons comment accompagner un nombre d'une indication d'incertitude ou de précision >>>

Anglais: measurement uncertainty

Vocabulaire

Les chiffres certains et le chiffre incertain forment les chiffres significatifs.

Les zéros de tête ne sont pas des chiffres significatifs; alors que ceux de queue le sont.

Anglais: all definite digits and the first doubtful digit are all considered as significant.

Leading zeros are not significant figures; trailing zeros are significant figures.

Niveau collège

Mesure – Exemple
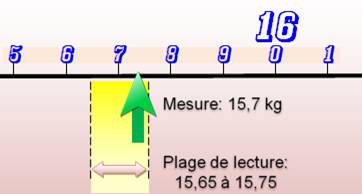
Lecture de la mesure Sur cette balance, l'aiguille dépasse légèrement la graduation 15,7. On lit tout de même: 15,7 kg. Chaque fois que l'aiguille s'arrêtera autour du 0,7 (plage en jaune), on lira 15,7 kg en sachant que la mesure est comprise entre 15,65 kg et 15,75 kg. Soit, une incertitude égale à la moitié du dixième de kilogramme.
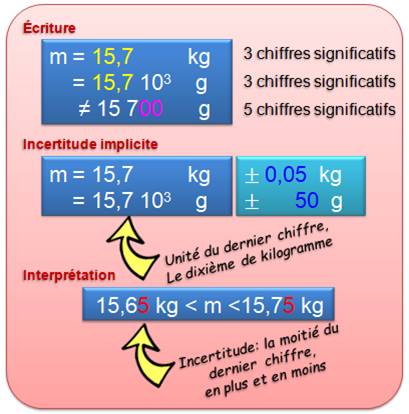
Interprétation Lorsque la mesure indique 15,7 kg, l'intention est de signifier que la lecture de la plus petite graduation de la balance est le dixième de kg, soit la centaine de grammes. On dit que la mesure est faite avec trois chiffres significatifs, ou encore, un chiffre significatif après la virgule. Lire 15,700 kg ou encore 15 700 (cinq chiffres significatifs) serait abusif, nous n'avons pas accès à cette précision sur notre balance. Incertitude Lorsqu'on veut expliciter l'incertitude, on peut soit mentionner sa valeur en plus et en moins; ou alors, donner une inégalité (dit: intervalle de confiance).

Demi-unité du dernier chiffre exprimé
Spécification	Les manuels indiquent parfois la manière d'interpréter la mesure: En l'absence d'autres indications, on convient que l'incertitude porte sur le dernier chiffre exprimé et vaut une demi-unité de ce chiffre. Lorsque la valeur d'une grandeur est fournie sans incertitude, cette dernière est, par convention, égale à une demi-unité du dernier chiffre exprimé. On appelle incertitude absolue une demi-unité du dernier chiffre affiché.
Historique	L'erreur commise, en plus ou en moins, est égale à une demi-unité du dernier ordre conservé – Bézout (1810)
Que signifie ces expressions	Interprétation On entend par unité, l'unité de mesure qui correspondrait à ce nombre, comme s'il était converti en un nombre sans sa virgule. Exemple pas à pas 5,4 g => sans virgule: 54 décigrammes (dg) => précision: la moitié de 1dg = 0,5 dg => 54 dg 0,5 dg => 5,4 g 0,05 g Autres exemples 123,00 m² => (123,00 0,005) m² On note ici que les deux 0 sont des chiffres significatifs. U1 = 730 mV => 729,5 mV < U1 < 730,5 mV U2 est exprimé avec 2 chiffres significatifs. U2 = 0,73 V => 0,725 V < U2 < 0,735 V U1 est exprimé avec 2 chiffres significatifs.
Compréhension	Le mot unité peut prêter à confusion. Ici, il s'agit bien de l'unité de mesure, mais certains peuvent penser à l'unité d'un nombre (le dernier chiffre d'un nombre entier) et ne plus rien y comprendre. Même si le lecteur pense à l'unité de mesure, pour lui c'est, par exemple, le kilogramme, mais pas le dixième de kilogramme. Le lecteur est perdu.
Que dire ? Suggestions:	Par convention, on dit que le dernier chiffre significatif est connu à 0,5 près. L'incertitude absolue L sur la mesure est égale à une demi – unité du dernier rang affiché par l'instrument. L'incertitude correspond à la moitié de l'unité de mesure correspondant à la position du dernier chiffre exprimé.

Voir Demi

Merci à Corinne C. pour ses remarques constructives

Niveau lycée

Paramètres associés à une mesure
Définition	Mesurer une grandeur consiste à rechercher la valeur de cette grandeur et à lui associer une incertitude afin de pouvoir qualifier la qualité de la mesure. Comment caractériser cette qualité? valeur mesurée comparée à la valeur vraie; résultat, précision, incertitude, erreur de mesure.
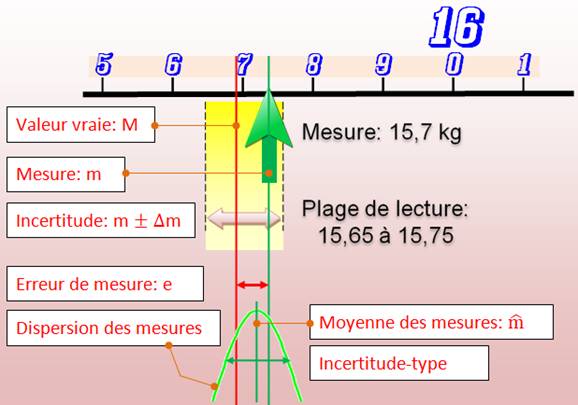
Erreur	L'erreur de mesure est la différence entre la valeur mesurée et la valeur vraie. Elle peut être aléatoire (quelconque) ou répétitive (toujours la même: biais de mesure). L'instrument de mesure est fidèle s'il donne toujours des indications voisines pour plusieurs mesures
Résumé des paramètres liés à une mesure
Calcul de la moyenne et de l'écart-type
Composition des incertitudes absolues	Incertitude absolue sur la somme = somme des incertitudes absolues
Composition des incertitudes relatives		Incertitude relative sur le produit = somme des incertitudes relatives

Anglais: Absolute uncertainty and percentage undertainty

Voir Moyenne, écart type …

Quelques remarques d'écriture
Homogène Lorsque l'incertitude est précisée, le nombre doit être du même ordre.	15,75623 0,002 15,756 0,002
Notation Dans les textes scientifiques, la valeur entre parenthèse indique l'incertitude sur les derniers chiffres. C'est en général l'écart type.

Précision et justesse
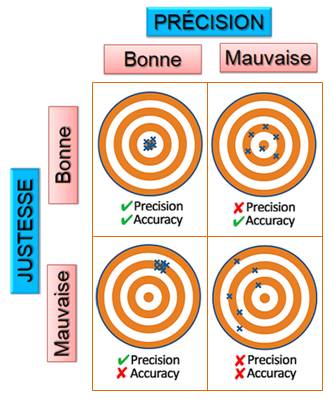
Précision d'une valeur – Precision = incertitude qui lui est attachée. Plus un résultat ou un calcul est précis, plus le nombre de chiffres significatifs est grand et plus l'intervalle de confiance est petit. Justesse – Accuracy = Erreur de mesure minimale. La valeur vraie étant généralement inconnue, la justesse est difficile à apprécier. On s'en approche, en faisant de nombreuses mesures ou encore en pratiquant des approches variées.
Qualité des appareils de mesure	Fidélité Un appareil de mesure est fidèle s'il donne un même résultat pour plusieurs mesures dans les mêmes conditions. Exactitude Un appareil de mesure est exact si les résultats sont justes, si l'erreur de mesure est minimale.

Précision et justesse sont souvent confondues dans le langage, en français comme en anglais.

Anglais: Acurracy: justesse, exactitude / Pinpoint accuracy: précision chirurgicale

Suite	Ordre de grandeur Arrondi Résolution Voir haut de page
Voir	Nombres décimaux Nombres n-ronds Ordre de grandeur Unités Virgule flottante
Sites	Erreur de mesure – Wikipédia Nombres, mesures et incertitudes – éduscol Mesure, erreur, incertitude*** – Martin Vérot – pdf 67 pages – Niveau supérieur Averaging, Errors and Uncertainty – Penn University
Cette page	http://villemin.gerard.free.fr/aNombre/FORMATIO/Incertit.htm