|
Édition du: 04/06/2023 |
|
INDEX |
Nombres et théorème de RAMSEY |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
RAMSEY R(4,4) = 18 et R(4, 5) = 25 Déjà avec ces
petits nombres, il n'est pas aisé de recenser tous les cas. Heureusement
l'algèbre vient à notre secours. |
||
|
|
Sommaire de cette page >>> R(4, 4) – Borne inférieure >>> R(4, 4) – Borne supérieure >>> Assemblée de 18 personnes >>> R(4,5) = R(5,4) = 25 |
Débutants Glossaire |
|
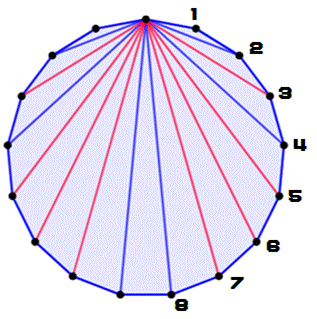
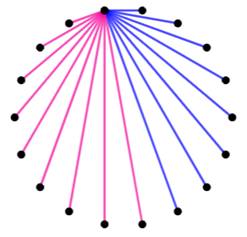
Borne inférieure Avec 17 sommets, il est possible de colorier le graphe
complet avec deux couleurs sans jamais créer un quadrilatère complet (quatre
sommets et toutes les arêtes possibles). La figure montre le principe de la coloration:
|
Pentagone à 17 côtés
Méthode du coloriage en
rouge et bleu des arêtes issues de chaque sommet. |
||
|
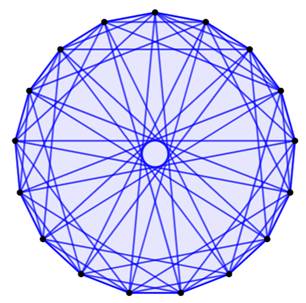
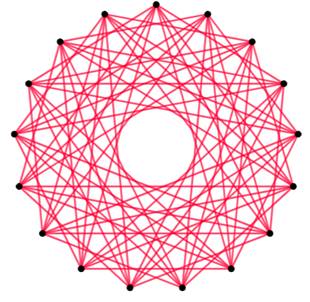
Sur ces deux figures complémentaires, aucun
quadrilatère bleu ou rouge ne contient ses diagonales. Donc pas de R4. Le nombre R(4, 4) est plus grand que 17. |
Pentagone à 18 côtés: les deux
graphes complémentaires rouge et bleu
Avec 17 sommets, il est
naturellement possible de créer des quadrilatères complets. Mais, parmi tous
les graphes colorés possibles, il existe au moins un
cas où il n'y a pas de quadrilatère complet. Celui illustré ci-dessus. Or, le nombre de Ramsey
exige que, quel que soit le coloriage, il y ait toujours un quadrilatère
complet. Ce n'est donc pas avec 17, et R(4, 4) est donc plus grand que 17. |
||
|
Borne supérieure On se réfère à l'inégalité
des nombres de Ramsey. Voir Table
des valeurs |
R(4, 4) ≤ R(3, 4) + R(4, 3) = 9 + 8 = 18 On a donc: 17
< R(4, 4) ≤ 18 => R(4, 4) = 18
|
||
|
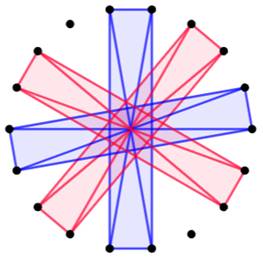
Exemple de tracé Avec 18 sommets, il est possible de créer
plusieurs quadrilatères complets. Il est même impossible de ne pas en créer un. Tracé inévitable Illustrer l'apparition inévitable d'un
quadrilatère complet n'est pas simple. Jeux On peut imaginer un jeu à deux. Les dix-huit
points sont dessinés en un cercle approximatif. Chaque joueur dessine un
trait rouge pour l'un et bleu pour l'autre. Le premier qui dessine un quadrilatère complet de
sa couleur a perdu. Avec six sommets, le jeu est connu comme le jeu de Sim |
Exemple de tracé de quadrilatères
complets avec 18 sommets
Quatre
quadrilatères complets. |
||
|
En terme de complémentaire Pour tout graphe d'au moins 18 sommets (R18),
soit G, soit son complémentaire Gc, contient un sous graphe
complet à quatre sommets (R4). |
En résumé, on dit que:
Rk
est le graphe complet à k sommets |
||
|
Deux à deux Dans une assemblée de 18 personnes,
Quatre à quatre Dans une assemblée de 18 personnes, il est
toujours possible de trouver, au moins:
|
Avec 18 sommets
Au moins 8 sont d'une
couleur et 9 de l'autre. |
|
|
Un graphe complet à au moins 25 sommets R25
contient au moins un graphe complet R4 ou un graphe complet R5. |
Démonté en 1995 par Brendan
D. Mc Kay et Stanislaw P. Radziszowski >>> |
|
|
Historique Une borne inférieure fut trouvée en 1965 par
Kalbfleish en construisant un graphe avec 24 sommets. |
R(4, 5) ≥ 25 |
|
|
Une borne supérieure était connue dès 1955 –
Greenwood et Gleason |
R(4, 5) ≤ R(3, 5) + R(4, 4) – 1 = 14 + 18 – 1 = 31 |
|
|
Walker utilise la programmation linéaire pour compter les sous-graphes. |
R(4, 5) ≤ 27 |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/R44.htm
|
|