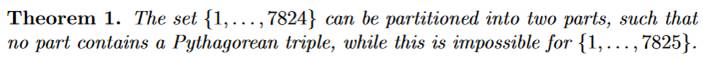|
|||||||||||||||||||||||||||||
![]()
|
Nombres et couleurs Partition (coloration) des nombres Donnez
une couleur à chacun des nombres entiers de façon telle que les nombres
impliqués dans une opération soit tous de couleurs différentes. Un peu comme
le célèbre problème des quatre
couleurs pour les cartes, mais appliqué au nombre entiers. Ces
questions font partie de la théorie
de Ramsey, théorie générale qui vise à découvrir les structures
apparaissant dans des ensembles suffisamment larges. 2016:
démonstration par ordinateur pour la bi-coloration des triplets de Pythagore >>> |
|
|
||
|
Colorier les nombres selon une règle donnée Idée
curieuse de vouloir colorier chaque nombre de couleurs différentes. Oui, mais
une quantité donnée de couleurs seulement. Ça ne
serait pas drôle sans une règle de coloriage. La plus
simple est la suivante:
|
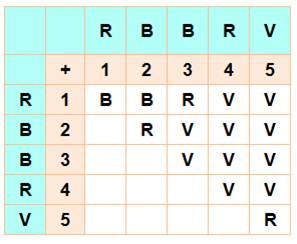
Aucun triplet monochromatique avec 3 couleurs
Cette table d'addition colorée montre que dans tous les cas: a + b =
c, les trois nombres ne sont pas de la même couleur. |
|
|
En 1916,
Issai Schur (1875-1941) a démontré que: Avec un nombre fini de couleurs et la fonction a + b = c, il est
toujours possible d'obtenir un triplet monochromatique. Plus précisément Pour tout nombre k > 0, il existe un nombre S(k), tel que [1, S(k)]
peut être partitionné en k parties sans qu'une des parties ne contienne à la
fois a, b et c, alors que a + b = c. Par contre, cela est possible pour [1,
S(k) + 1]. S(k) est
un nombre de Schur. |
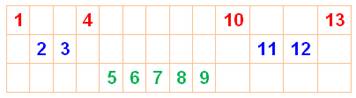
Avec
trois couleurs, il est possible d'éviter le triplet monochromatique jusqu'à
13, mais avec 14, impossible d'y échapper. Coloriage pour n de 1 à 13
Avec ce coloriage à trois couleurs, aucun triplet monochromatique. |
|
|
|
||
|
Vocabulaire Partition se réfère à la création d'autant d'ensembles de
nombres que de couleurs considérées. Avec r couleurs, on parle de r-partition. Si la r-partition
présente toujours une solution monochromatique (comme vue ci-dessus), elle
est dite r-régulière |
Exemple Trois
couleurs créent une 3-partition de la l'équation a + b = c. Comme il
est impossible d'échapper à un triplet monochromatique, l'équation est
3-régulière. Autre exemple L'équation
a + 2b – 5c = 0 est 3-régulière, mais pas 4-régulière. |
|
|
Théorème de Rado En 1933,
Tibor Rado (1895-1965) démontre que: L'équation a1x1 + a2x2 + …
+ anxn = 0 est régulière si et seulement si la somme d'un
sous-ensemble des coefficients non nuls est nulle. |
Conjecture de Rado Il émet
aussi une conjecture qui est prouvée dans les cas triviaux n = 1 et n = 2,
mais pas au-delà. En gros:
jusqu'à un niveau n de l'équation, il existe un nombre k (fonction de n) tel
que si cette équation est k-régulière, alors elle est régulière. |
|
|
|
||
|
Attribuons
une couleur aux nombres de façon telle que les trois nombres impliqués dans
un triplet de Pythagore ne
soient pas de la même couleur. Est-ce possible? En 2013,
on ne sait toujours pas si c'est possible pour deux couleurs. On ne sait pas
colorer les nombres de façon telle qu'il n'existe aucun triplet
monochromatique. En 2013,
Joshua Cooper et Chris Poirel, réussissent à colorier les nombres avec deux couleurs
jusqu'à 1344 sans avoir de triplet monochromatique. |
En mai
2016, Heule, Kullmann et Marek déclarent avoir démontré le problème des triplets bi-colorés de
Pythagore. Ils ont
montré qu'il est possible de colorier les nombres sans triplets monochromatique
jusqu'à 7 824 (nombre de Schur), mais
avec un de plus, c'est impossible: il y aura toujours un triplet d'une seule
couleur quelque part. La preuve fait
un emploi massif d'ordinateurs: 800 processeurs en parallèle sur une période
de 2 jours. 200
téraoctets générés. C'est la plus grande preuve informatique jusqu'en
2016. Évidemment, la
recherche met en jeu des propriétés qui permettent de réduire sensiblement
l'exploration 102300 cas à explorer. Notez que ce
type de preuve établit des faits sans les expliquer. Pourquoi 7 824? |
|
Exemple de bi-partition (bi-coloration) et
comparaison aux triplets de Pythagore
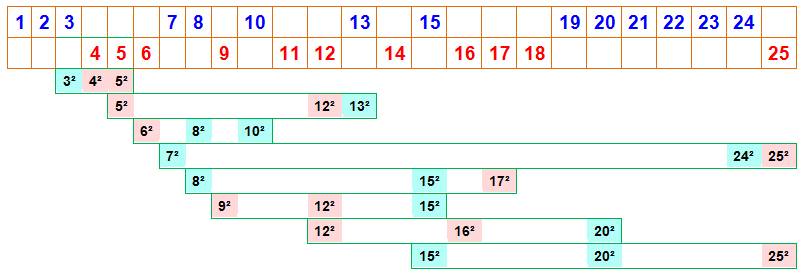
Voir Nombre
7 824 / Brève 57-1120
|
|
|
|
Is there a way to color Can the natural numbers be assigned
a2-coloring, so that no Pythagorean triple is monochromatic? The Boolean
Pythagorean triples problem was a conjecture relating to Pythagorean
triples which was shown to be false using a Computer-assisted proof in May
2016. The boolean
Pythagorean Triples problem has been a long-
standing open problem in Ramsey
Theory: Can the set
Note: Boolean ou booléen en français fait
référence au nombre 2 de la bi-partition. Création de deux ensembles: chaque
nombre est dans l'un ou dans l'autre. |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()