|
Édition du: 04/06/2023 |
|
INDEX |
Nombres et théorème de RAMSEY |
|||
|
EN BREF –
Tour d'horizon |
||||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES de RAMSEY En bref – Tour d'horizon
Alors que, la taille
de ces structures est connue pour les petits ensembles, elle reste un sujet
de recherches pour les plus grandes valeurs. On connait des formules
précisant l'encadrement de la taille. Les mathématiciens recherchent à le
réduire au maximum. La théorie de Ramsey trouve des applications dans
divers domaines: informatique, routage réseau, codes de correction d'erreurs;
cryptographie; réseaux sociaux, réseaux de communication, groupes
biologiques; etc. |
||
|
|
Sommaire de cette page >>> Nombres de Ramsey >>> Théorie de Ramsey >>> Tour d'horizon >>> Domaine et intérêt |
Débutants Glossaire |
Anglais : Ramsey numbers
|
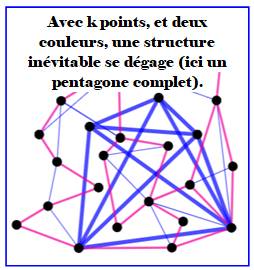
Du concret avant généralisation La figure montre six points dont certaines des
liaisons sont colorées en bleu ou en rouge. La théorie de Ramsey dit qu'à partir de six
points, il est impossible de colorier toute cette figure sans faire
apparaitre un triangle monochrome (bleu ou rouge). Le triangle étant la figure à trois points tous
réunis est nommé R3. Les six points tous réunis est nommée R6.
Il s'agit d'un hexagone complet
ou graphe complet à six sommets. Et, on note le nombre de Ramsey R(3, 3) = 6. Le nombre de Ramsey 6 est la quantité minimale de
points à partir de laquelle il est inévitable de trouver un triangle
monochrome. Avec quatre points tous réunis, on sait que le
nombre de Ramsey est: R(4, 4) = 18. En fait, on ne connait que très peu de ces
nombres de Ramsey. |
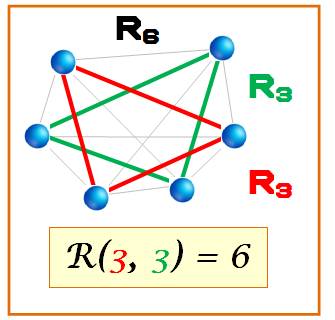
Six points tous réunis: hexagone
complet
Avec six sommets (R6),
il est possible de créer deux triangles (R3) distincts et de
couleurs différentes. Mais surtout, en coloriant
tous les traits avec deux couleurs, il est impossible
d'éviter un triangle rouge ou un triangle bleu. |
|
|
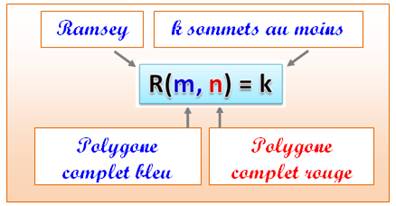
D'une manière générale, le nombre de
Ramsey R(m , n) est
la quantité k de sommets nécessaire et suffisante pour que l'un des deux
polygones complets bleu ou rouge existe inévitablement dans un polygone de k
sommets. Notez que l'on s'intéresse à des polygones de deux couleurs seulement. Avec k couleurs,
il s'agit des nombres de Ramsey généralisés: R(m, n, p, q ...). |
|
|
|
Approche Si on colorie en r couleurs les éléments d’une certaine
structure très grande, alors il existe une sous-structure assez grande pour
laquelle et au-delà de laquelle tous les éléments sont de la même couleur. Autrement dit, le désordre
complet n’existe pas. |
Plus précisément La théorie de Ramsey est l'étude de questions du
type suivant : étant donné une structure combinatoire (par exemple un graphe
ou un sous-ensemble
d'entiers), quelle doit être la taille de la structure pour garantir
l'existence d'une sous-structure (par exemple sous-graphe, sous-ensemble)
avec une propriété donnée ? |
|
|
Les nombres de
Ramsey sont un concept de mathématiques combinatoires qui se rapporte à
l'étude des graphes et à l'existence de certains modèles en leur sein. Ils ont
été introduits pour la première fois par le mathématicien britannique Frank
P. Ramsey en 1930. Les nombres de Ramsey fournissent une mesure de la taille
minimale qu'un graphe doit avoir pour garantir la présence d'un sous-graphe
ou d'une propriété particulière. En termes
simples, les nombres de Ramsey répondent à la question : Quelle doit être la
taille d'un graphe pour garantir la présence d'une structure ou d'une
propriété spécifiée ? Ces structures sont généralement définies en termes
d'arêtes ou de sommets colorés dans un graphe. Prenons un
exemple pour mieux comprendre ce concept. Supposons que nous ayons deux
couleurs, rouge et bleu, et que nous voulions connaître le nombre minimum de
personnes nécessaires à une fête pour s'assurer qu'il y a soit trois amis
communs (qui se connaissent tous) soit trois inconnus communs (qui ne se
connaissent pas tous). Ce problème peut être représenté à l'aide d'un graphe,
où les personnes sont les sommets et les segments entre eux représentent
s'ils sont amis (segment rouge) ou étrangers (segment bleu). Le nombre de
Ramsey, noté R(m, n), représente le plus petit nombre de sommets (ou de
personnes dans notre exemple) nécessaire dans un graphe complet (un graphe où
chaque paire de sommets est connectée) pour garantir la présence d'un
sous-graphe complet de taille m, tous avec des arêtes rouges, ou un
sous-graphe complet de taille n, tous avec des arêtes bleues. |
Les nombres de
Ramsey ont de nombreuses applications dans divers domaines des mathématiques,
de l'informatique et de la physique théorique. Voici quelques exemples: 1. Théorie des
graphes : les nombres de Ramsey sont fondamentaux dans la théorie des
graphes et ont des applications dans l'étude de l'existence de modèles ou de
structures particuliers dans les graphes. 2. Théorie du
codage : les nombres de Ramsey sont utilisés dans la théorie du codage
pour déterminer le nombre minimal d'éléments (par exemple, des symboles ou
des mots de code) nécessaires pour garantir l'existence d'un code de
correction d'erreur ou d'une propriété de code particulier. 3. Complexité
informatique : les nombres de Ramsey jouent un rôle dans la compréhension de
la complexité informatique de certains problèmes. Ils fournissent des limites
sur les ressources (telles que le temps ou l'espace) nécessaires pour
résoudre des problèmes dans des domaines tels que la théorie des graphes
informatiques et l'optimisation combinatoire. 4. Théorie de
Ramsey : Les nombres de Ramsey sont un sujet central de la théorie de Ramsey,
qui étudie l'émergence de l'ordre dans les structures mathématiques. La
théorie de Ramsey a des liens avec de nombreuses autres branches des
mathématiques, notamment la théorie des nombres, la théorie des ensembles et
la logique. 5. Réseaux
sociaux : les nombres de Ramsey trouvent des applications dans l'analyse
des réseaux sociaux et l'étude de propriétés telles que les cliques
(sous-graphes complets) ou la présence de communautés au sein d'un réseau. Dans l'ensemble,
les nombres de Ramsey sont un outil puissant pour comprendre l'existence de
modèles ou de propriétés spécifiques dans les graphes, et leurs applications
s'étendent à divers domaines des mathématiques et de l'informatique. |
||
|
|
|||
|
La théorie de Ramsey
est une branche de la combinatoire qui étudie l'émergence de l'ordre dans des
structures apparemment aléatoires. Explorons
quelques concepts et résultats clés de la théorie de Ramsey : 1. Limites et valeurs exactes : déterminer les
nombres exacts de Ramsey est un problème difficile, et les valeurs exactes ne
sont connues que pour les petits cas. Cependant, les chercheurs ont établi
des limites inférieures et supérieures pour les nombres de Ramsey sur la base
de techniques combinatoires, de méthodes probabilistes et d'outils
mathématiques avancés. Les bornes impliquent souvent des fonctions
exponentielles ou double-exponentielles des paramètres m et n. 2. Variations : la théorie de Ramsey s'étend
au-delà des graphes et peut être appliquée à diverses structures
combinatoires, telles que les hypergraphes, les systèmes d'ensembles, les
permutations, etc. Différentes variantes de la théorie de Ramsey explorent
des sous-structures, des colorations ou des arrangements géométriques
spécifiques. 3. Applications : la théorie de Ramsey fournit
des informations sur l'existence d'un ordre dans des systèmes apparemment
aléatoires et aide à établir des limites à la présence de modèles
spécifiques. 4. Problèmes ouverts : malgré des progrès
significatifs, de nombreux nombres de Ramsey sont encore inconnus. La
détermination de valeurs précises pour des nombres de Ramsey plus grands
reste un problème ouvert difficile en mathématiques. Les chercheurs
continuent d'explorer de nouvelles techniques, d'améliorer les limites et
d'étudier les propriétés des nombres de Ramsey. La théorie de
Ramsey fascine les mathématiciens depuis des décennies et ses liens profonds
avec diverses branches des mathématiques en font un domaine de recherche
actif. Il révèle l'ordre sous-jacent caché dans les structures et met en
lumière l'émergence de modèles dans des systèmes apparemment chaotiques. Voyons quelques
détails supplémentaires sur la théorie de Ramsey : 1. Théorème de Ramsey : L'un des théorèmes
fondamentaux de la théorie de Ramsey est le théorème de Ramsey, qui fournit
un cadre général pour comprendre l'émergence de l'ordre au sein de grandes
structures. Le théorème de Ramsey stipule que pour tout entier positif m et
n, il existe un nombre R (m , n) tel que tout graphe complet sur R( m, n)
sommets contiendra soit une m -clique, soit un ensemble n-indépendant. 2. Nombres de Ramsey et complexité de calcul : La
détermination des nombres de Ramsey exacts est connue pour être un problème
de calcul difficile. En fait, le calcul des nombres de Ramsey est classé
comme un problème d'optimisation combinatoire et relève du domaine des
problèmes NP-complets,
ce qui signifie que la recherche de solutions optimales nécessiterait un
temps exponentiel. 3. Limites pour les nombres de Ramsey : Les
chercheurs ont établi diverses limites pour les nombres de Ramsey. Pour les
petites valeurs de m et n, les valeurs exactes sont connues. Pour des valeurs
plus grandes, des limites inférieures et des limites supérieures sont
dérivées. Les bornes inférieures sont généralement obtenues à l'aide de
constructions qui garantissent l'existence de certaines sous-structures,
tandis que les bornes supérieures sont obtenues par des arguments
probabilistes ou des arguments récursifs. 4. Connexions à la théorie des graphes : la
théorie de Ramsey a des liens profonds avec la théorie des graphes. La
théorie explore la présence de sous-structures (cliques et ensembles
indépendants) dans les graphes. De nombreux concepts théoriques des graphes,
tels que le nombre chromatique, la coloration des arêtes et le théorème de
Turán, sont liés à la théorie de Ramsey. 5. Théorème d'Erdős-Szekeres : Le théorème
d'Erdős-Szekeres est un résultat célèbre de la théorie de Ramsey qui
fournit des limites pour les sous-séquences monotones dans des séquences de
nombres. Il stipule que pour tout entier positif r et s, il existe un nombre
N(r, s) tel que toute séquence de N(r, s) nombres réels distincts contient
soit une sous-séquence monotone croissante de longueur r, soit une
sous-séquence monotone décroissante de longueur s. 6. Généralisations : La théorie de Ramsey a été
étendue à divers domaines au-delà des graphes. Par exemple, il existe des
nombres de Ramsey hypergraphiques, qui considèrent l'existence d'hypergraphes
avec des propriétés spécifiques. De plus, la théorie de Ramsey a des liens
avec la théorie de la combinatoire infinie et la théorie des ensembles. La théorie de
Ramsey continue d'être un domaine de recherche actif, les mathématiciens
cherchant à découvrir de nouvelles limites, à étudier les variations de la
théorie de Ramsey et à explorer les liens avec d'autres branches des
mathématiques et de l'informatique. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
||
|
Suite |
|
|
|
Voir |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/EnBref.htm
|
|