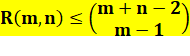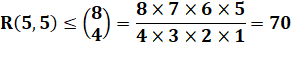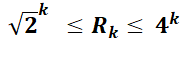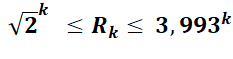|
Édition du: 04/06/2023 |
|
INDEX |
Nombres et théorème de RAMSEY |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombres de RAMSEY
Il existe des
relations exprimant les bornes des nombres de Ramsey. Celles-ci sont propices
au calcul des petits nombres de Ramsey. |
||
|
|
Sommaire de cette page >>> Théorème de Ramsey >>> Principales propriétés >>> Recherche des bornes >>> Méthodes de calcul – Idée |
Débutants Glossaire |
|
Soit deux
nombres entiers positifs m et n. Alors, il existe
un entier positif s, qui est fonction
de m et n, tel que dans le graphe Rs
on trouve inévitablement un sous-graphe monochrome Rn ou Rm.
Autrement-dit: en
coloriant le graphe complet avec deux couleurs, il est impossible d'éviter un
sous-graphe monochrome complet Rm ou Rn. Le nombre de Ramsey R(m,
n) Les graphes Ri sont des graphes
complets. Le théorème vaut pour deux couleurs; il est
généralisable à k couleurs. |
|
|
|
Propriétés simples à démontrer |
Symétrie: R(m, n) = R(n, m) Cas 1: R(1, n) = R(n, 1) = 1 Cas 2: R(2, n) = R(n, 2) = n |
|
|
Inégalité avec les coefficients du
binôme La borne supérieure est généralement très
surestimée par cette formule. |
Exemple
On sait rédiuire cette valeur à 48. |
|
|
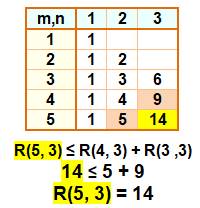
Inégalité avec nombres de Ramsey
voisins inférieurs Exemple
|
R(m, n) ≤ R(m–1, n) + R(n, n–1) Exemples R(3, 3) ≤ R(2, 3) + R(3, 2) = 3 + 3 = 6 (vrai) R(3, 5) ≤ R(2, 5) + R(3, 4) = 5 + 9 = 14 (vrai) R(5, 5) ≤ R(3, 4) + R(4, 3) = 9 + 9 = 18
(vrai) R(3, 7) ≤ R(2, 7) + R(3, 6) = 7 + 18 = 25
pour 23 R(3, 8) ≤ R(2, 8) + R(3, 7) = 8 + 23 = 31
pour 28 R(3, 9) ≤ R(2, 9) + R(3, 8) = 9 + 28 = 37
pour 36 |
|
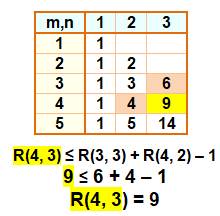
Cas particulier Si R(m–1, n) et R(n, n–1)
sont pairs, alors => Exemple
|
R(m, n) ≤ R(m–1, n) + R(n, n–1) – 1 Exemples R(3, 4) ≤ R(2, 4) + R(3, 3) – 1 = 4 + 6 – 1 = 9
(vrai) R(3, 6) ≤ R(2, 6) + R(3, 5) – 1 = 6 + 14 – 1 = 19
pour 18 R(4, 5) ≤ R(3, 5) + R(5, 5) = 14 + 18 – 1 = 31 pour 25 |
|
Cas m = n
|
R(m, m) ≤ 4 × R(m, m – 2) + 2 Exemple R(5, 5) ≤ 4 × R(5, 3) + 2 = 4 × 14 + 2 =
58 On connait une borne moins élevée: 48. |
|
Principe de calcul |
Ces deux dernières formules indiquent la borne
supérieure. Reste à trouver la borne inférieure. Pour les
petites valeurs, un exemple de coloriage suffit généralement. |
|
Premières estimations Erdös |
|
|
|
Estimation actuelles 2023 |
|
|
Suite
et explications en
Bornes et historique
|
Le calcul de la valeur
exacte des nombres de Ramsey, tels que R (5, 5), est un problème difficile,
et trouver les valeurs exactes de la plupart des nombres de Ramsey est une
question de recherche ouverte. Cependant, on peut expliquer une approche
générale que les chercheurs utilisent pour trouver des limites inférieures
pour les nombres de Ramsey. Pour calculer
une borne inférieure pour R(5, 5), nous
devons trouver un graphe avec un certain nombre de sommets qui ne contient
pas un sous-graphe complet de taille 5 (clique) ni un ensemble indépendant de
taille 5. Si nous trouvons un tel un graphe, cela implique que le nombre de
Ramsey R(5, 5) est au moins le nombre de sommets dans ce graphe. Pour les petites
valeurs, la recherche pas dessin est faisable. Mais, elle devient impossible
pour les plus grandes valeurs. Alors, la
méthode la plus courante pour trouver les bornes inférieures pour les nombres
de Ramsey consiste à utiliser une technique appelée la méthode probabiliste,
introduite par le mathématicien Paul Erdős. Cette méthode consiste à
construire un graphe aléatoire avec certaines propriétés et à montrer que la
structure souhaitée (dans ce cas, une 5-clique ou un ensemble 5-indépendant)
est peu susceptible d'exister dans le graphe. La recherche de limites supérieures pour les nombres de Ramsey
est également un domaine de recherche actif, où les mathématiciens essaient
de construire des graphiques contenant les structures souhaitées. L'étude des
nombres de Ramsey et de leurs limites reste un sujet intrigant et stimulant
en mathématiques. |
Voici un aperçu
général de la façon dont la méthode probabiliste peut être appliquée pour
trouver une borne inférieure pour R(5, 5) : Supposons un modèle
de graphe aléatoire : Commencez par considérer un graphe aléatoire avec un
certain nombre de sommets et d'arêtes. Les arêtes peuvent être ajoutées entre
les sommets avec une certaine probabilité. Estimer la
probabilité : Calculez la probabilité qu'un sous-graphe spécifique, tel qu'un
ensemble 5-clique ou 5-indépendant, existe dans le modèle de graphe
aléatoire. Il s'agit d'analyser la probabilité que les conditions requises
soient satisfaites. Montrez que la
probabilité est faible : utilisez la théorie des probabilités et des
arguments combinatoires pour démontrer que la probabilité que le sous-graphe
souhaité existe dans le modèle de graphe aléatoire est très faible. Cela se
fait généralement en analysant le nombre attendu de sous-graphes et en montrant
qu'il est petit. Fixer une borne
inférieure : si la probabilité du sous-graphe souhaité est très faible,
cela implique qu'un graphe avec le nombre spécifié de sommets ne contient pas
le sous-graphe. Par conséquent, le nombre de Ramsey R(5, 5) est au moins le
nombre de sommets dans le graphe construit. En employant des
techniques sophistiquées et en analysant les probabilités impliquées, les
mathématiciens ont pu établir des limites inférieures pour les nombres de
Ramsey. Cependant, le
calcul de valeurs précises pour des nombres de Ramsey plus grands reste un
problème ouvert, et la valeur exacte de R(5, 5) est actuellement inconnue. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/Calculs.htm
|
|