|
Édition du: 04/06/2023 |
|
INDEX |
Nombres et théorème de RAMSEY |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
Les graphes sont
un excellent moyen de visualiser et de comprendre la théorie de Ramsey. On
s'intéresse :
La théorie de
Ramsey cherche à définir la taille du graphe telle qu'il est inévitable d'y
trouver un sous-graphe monochrome complet de m ou n sommets. Ce nombres est
noté: R(m, n). |
||
|
|
Sommaire de cette page >>> Approche avec le carré >>> Cas du pentagone >>> Cas de l'hexagone |
Débutants Glossaire |
|
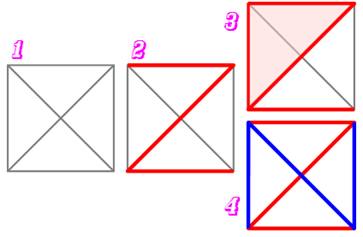
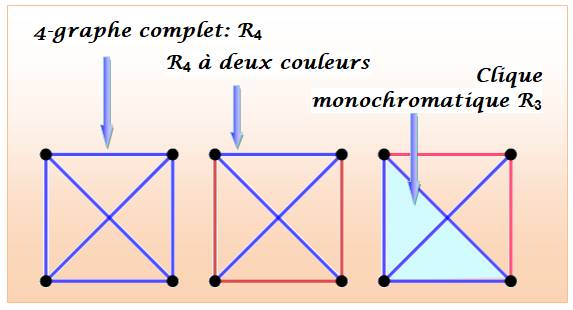
Cas du carré On considère un carré et ses diagonales (1). On se propose de colorier les arêtes de deux
couleurs: rouge et bleue. Existe-t-il une façon qui évite de créer un
triangle d'une couleur où de l'autre ? Solution En 2), une configuration ou les traits rouges ne
créent pas de triangle. En 3), un autre trait rouge et, alors, un
triangle rouge est créé. En 4), un tracé bleu tel qu'il n'existe aucun
triangle rouge ou bleu. |
Avec un carré, il est possible de créer un
dessin (4) sans triangle monochrome (d'une seule couleur). |
|
|
Profitons ce cette approche pour introduire du
vocabulaire. Un graphe complet
est un graphe dont tous les sommets sont reliés entre eux. Avec quatre sommets, il a y donc six arêtes. Un carré avec ses diagonales est un carré complet. On le nomme R4. Un triangle (qui n'a pas de diagonale) est naturellement
complet. On le nomme R3. |
Un graphe est constitué
d'une paire d'ensembles:
Deux graphes sont dits complémentaires
s'ils ont les mêmes sommets et des ensembles d'arêtes disjoints dont l'union
est constituée de toutes les arêtes possibles joignant leurs sommets. Chacun des graphes est appelé complément de l'autre. Le complémentaire du
graphe G est noté Gc. >>> |
|
Les graphes sont
parfois notés Kn, pour éviter une confusion
avec le nombre de
Ramsey R(n, n) parfois abrégé en R(n).
|
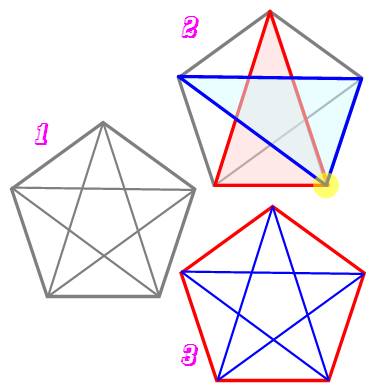
Cas du pentagone On considère un pentagone et ses diagonales (1).
Il n'est pas nécessaire qu'il soit régulier On se propose de colorier les arêtes de deux
couleurs: rouge et bleue. Existe-t-il une façon qui évite de créer un
triangle d'une couleur ou de l'autre ? Solution En 2), une configuration avec deux triangles mais
avec un sommet commun (jaune) En 3), une figure où tous les traits sont
coloriés en rouge et bleu et où aucun triangle n'est formé Conclusion Comme pour le carré, avec le pentagone, il existe
une manière de colorier qui évite la formation de triangles. |
Avec deux couleurs dans un pentagone,
il est possible de ne pas créer de triangles monochromes. |
|
|
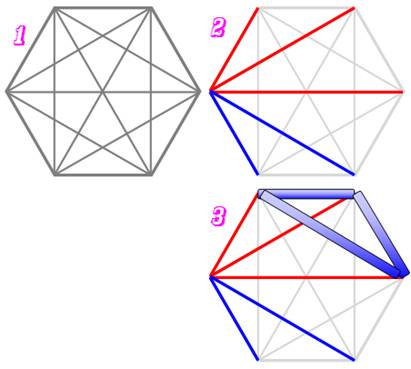
Cas de l'hexagone On considère un hexagone et ses diagonales (1).
Il n'est pas nécessaire qu'il soit régulier On se propose de colorier les arêtes de deux
couleurs: rouge et bleue. Existe-t-il une façon qui évite de créer un
triangle d'une couleur ou de l'autre ? Solution En 2), une configuration déduite du principe des
tiroirs qui dit que: avec 5 traits de 2 couleurs, alors au moins trois sont
de la même couleur. Choisissons le rouge pour notre exemple. En 3) si on ne veut pas créer de triangles
rouges, les traits reliant les arêtes rouges ne peuvent être complétés que
par des traits bleus. Or ces trois nouveaux traits forment un triangle bleu ! Conclusion Contrairement au carré et au pentagone, avec un
hexagone, il est impossible d'éviter de créer un triangle monochrome. |
Avec deux couleurs dans un
hexagone, il est impossible de ne pas créer un triangle monochrome. |
|
|
Nombre de Ramsey Avec six sommets, et c'est la quantité minimale,
il est impossible d'éviter les
triangles monochromes. |
On note R(3, 3) le plus petit nombre de sommets qu'un
graphique doit avoir pour que dans toute coloration rouge-bleu, il existe
soit un triangle (R3) rouge ou triangle (R3) bleu. Ce nombre R(3, 3) est appelé nombre de Ramsey. |
|
Voir D'autres exemples de graphes
sur la pages spécifiques en R(k, k)
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/Graphes.htm
|
|