Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 04/06/2023 M'écrire Brèves de Maths

INDEX Graphe Topologie Géométrie Logique Dénombrement Jeux	Nombres et théorème de RAMSEY
	Petits Nombres (Intro.)	Valeurs – Table	EN BREF
	Principe des tiroirs	Propriétés et calculs	R(3, 3) = 6	R(3, 3, 3)
	Assemblée	Bornes – Historique	R(3, 4) = 9	R(5, 3) = 14
	Graphe	Ramsey – Biographie	R(4, 4) = 18

Faites un double-clic pour un retour en haut de page

Nombres de Ramsey R(3,4) = R(4,3)= 9 Utilisation de l'inégalité pour la borne supérieur R(3, 4) ≤ 9 et d'un exemple de tracé pour la borne inférieure R(3, 4) > 8. Ce qui prouve que R(3, 4) = 9.
	Sommaire de cette page >>> R(3, 4) – Borne inférieure >>> R(3, 4) – Borne supérieure >>> Graphes complémentaires	Débutants Dénombrement Glossaire Combinatoire

R(3, 4) – Borne inférieure		haut
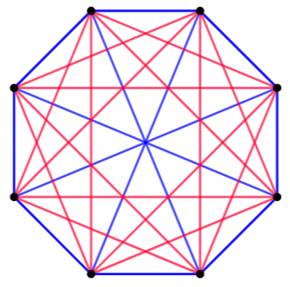
Borne inférieure Avec huit sommets, il est possible de colorier entièrement le graphe avec deux couleurs sans former de triangle ni de carré complet. On rappelle que les points de croisement des diagonales ne sont pas des sommets. Notez qu'en prenant un sommet sur deux, on crée des carrés, mais pas leurs diagonales. Le nombre de Ramsey (3, 4) est supérieur à 8.	Octogone Avec huit sommets, malgré tous les tracés, aucun triangle bleu et aucun quadrilatère complet rouge (et inversement pour les couleurs).

R(3, 4) – Borne supérieure			haut
Borne supérieure On se réfère à l'inégalité valable dans le cas des nombres pairs.	R(3, 4) ≤ R(2, 4) + R(3, 3) – 1 = 4 + 6 – 1 = 9 8 < R(3, 4) ≤ 9 => R(3, 4) = 9
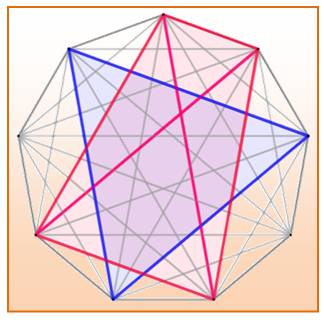
Exemple de tracé Avec neuf sommets, il est possible dessiner un triangle bleu et un quadrilatère rouge (ou inversement). Notez que, comme il ne reste que deux sommets, il est impossible de dessiner un autre triangle ou un autre quadrilatère. Bien sûr, il est possible de trouver d'autres configurations par rotation. Remarque: pour R(3, 4), il suffit qu'il soit possible de dessiner un triangle monochrome OU une quadrilatère complet monochrome pour valider le nombre. En résumé, on dit que: Rk est le graphe complet à k sommets		Ennéagone Avec neuf sommets, il est possible de tracer un triangle bleu OU un quadrilatère complet rouge.

Graphes complémentaires		haut
Définition Deux graphes sont dits complémentaires s'ils ont les mêmes nœuds et des ensembles d'arêtes disjoints dont l'union est constituée de toutes les arêtes possibles joignant leurs nœuds. Chacun des graphes est appelé complément de l'autre. Le complémentaire du graphe G est noté G^c. Exemple Dans l'octogone ci-dessus, les graphes bleu et rouge sont complémentaires.	Cas de R(3, 4) = 9 Un graphe G de R(3, 4) sommets est tel qu'il contient soit un graphe R4 soit son complémentaire contient un graphe R3. Autre formulation Tout graphe dichromatique G de R(3, 4) sommets, alors G contient soit R4 d'une couleur ou R3 de l'autre couleur.

Haut de page (ou double-clic)

Retour	Ramsey: R(3, 3) = 6
Suite	Ramsey: R(4, 4) = 18
Voir	Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ	Énigmes et paradoxes Graphe de Delaunay Intelligence artificielle Jeux – Index Logique formelle Percolation Relier les points d'un seul coup de crayon Topologie – Glossaire Tour de Brahmâ
Sites	Voir Références en page d'introduction
Cette page	http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/R43.htm