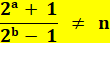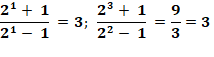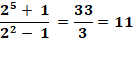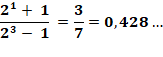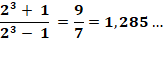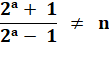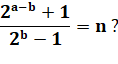|
||||||||||||||||||||||||||||
![]()
|
Formes
en an
+ 1 a2
+ 1 |
|
|
||
|
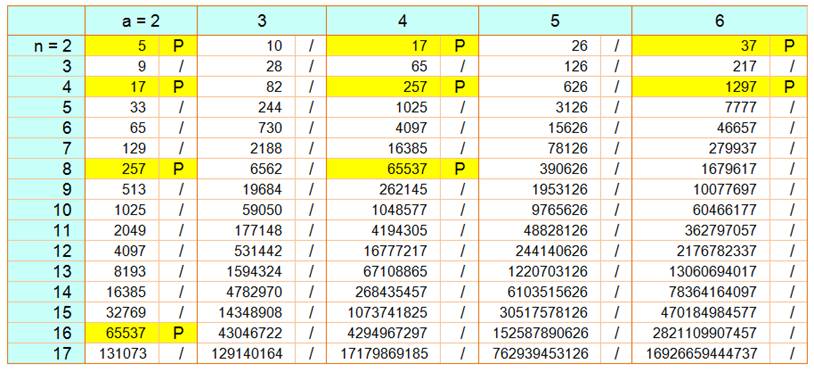
Démontrer que si an
+ 1 représente un nombre premier, a et n étant
supérieur à 1 |
Alors n est une puissance de 2. |
|
|
Si a > 1 alors |
an + 1 > 2 |
|
|
Si an + 1 est
premier |
alors an + 1 est impair, car tous les
premiers supérieurs à 2 sont impairs. |
|
|
Si an + 1 est
impair |
alors an est pair et a, lui-même est pair. |
|
|
Supposons que n ne soit pas
une puissance de 2 |
Alors n = premier ou produit
de premier selon le théorème
fondamental de l'arithmétique |
|
|
1) Supposons que n = p (donc
impair), alors notre forme se factorise |
an + 1 = (a – 1) (an–1 – an–2
+ ... – a + 1) |
|
|
La possibilité de
factorisation montre que cette forme
n'est pas première |
Contradiction avec notre
hypothèse. Supposition rejetée: n n'est
pas premier pur |
|
|
2) Supposons que n est un
produit de premiers (sans 2). Isolons
un des facteurs premiers p. Nous avons n = k . p Aussi bien p que k sont
impairs. Ce qui autorise la factorisation |
an + 1 = (an/p ) p + 1 = (ak
) p + 1 = (ak
– 1) ( ... ) |
|
|
À nouveau, factorisation |
Contradiction et la
supposition que n ne soit pas une puissance de 2 est fausse. |
|
|
|
|
|
|
|
|
|
|
|
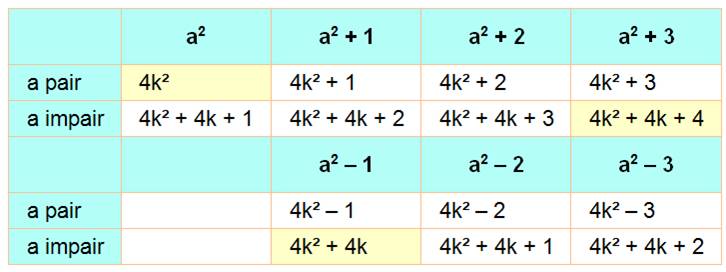
Les nombres a² + 3 pour a pair et a² + 1 pour a impair sont divisibles
par 4.
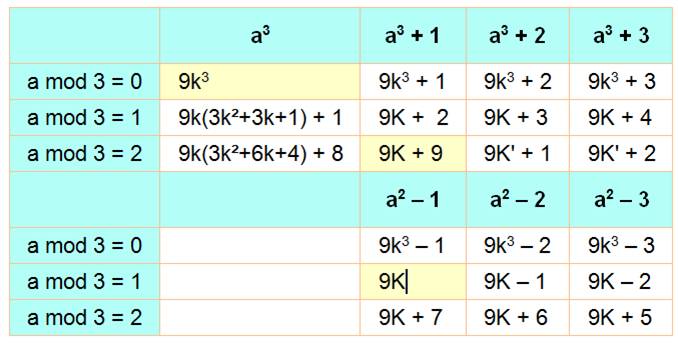
a3 est divisible par 9 si a l'est; a3 + 1 est divisible par 9 si a = 2 mod = 3; et a3 – 1 est divisible par 9 si a = 1 mod = 3. |
|
Forme de a² + 1 en a² – 2
|
Pour
tout entier a, a²+ 1 est de la forme 4k + 1 ou 4k + 2. Si a est pair, a² +
1 = (2h)² + 1 = 4h² + 1 = 4k + 1. Si a est impair,
a² + 1 = (2h + 1)² + 1 = 4h² + 4h + 2 = 4k + 2. Pour
tout entier a, a²- 2 n'est pas divisible par 4. Si n est divisible
par 4: n = 4q et a² - 2 = 16q² - 2, non divisible. Si n n'est pas
divisible par 4: n = (4q + r)²- 2 = 16q² + 8qr + r² - 2
|
|
Divisibilité
de 2a + 1 par 2b – 1
|
|
|
|
|
|
|
|
|
|
|
|
Démonstration |
|
|
|
|
|
|
|
|
Non divisible. |
|
|
|
|
|
|
|
|
|
|
|
Le numérateur est plus grand
que le dénominateur: pas divisible. |
|
|
|
|
|
|
|
|
|
|
|
a – b = a' tant que cette entité
est plus grande que b. |
|
|
|
Nous sommes ramenés au
deux cas précédents. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Puissanc/Exposant/Formanp1.htm |
![]()