|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mono: une bille
est plus lourde (ou plus légère) Ambi: une
bille est plus lourde ou plus légère sans
que nous le sachions a priori |
![]()
|
Énigme de la pesée des NEUF PIÈCES ou BILLES, BOULES, BALLES Exemple de pesée très simple avant d'aborder la
résolution des énigmes plus complexes avec douze
billes. Vous savez trouvez l'intrus parmi trois billes, vous savez le faire pour
toute puissance de 3 comme 3x3 = 9.
Avec cette énigme, l'intrus est un objet que nous savons être plus lourd (ou plus léger). Avec l'énigme des
douze balles, nous ne savons pas si l'objet est plus
lourd ou plus léger. |
|
|
||
|
Cas du problème des
neuf pièces Le
problème des neuf pièces apparait dans la
littérature en 1945 dans American Mathematical Monthly par E. D. Schell. Les
neuf pièces pèsent la même chose, sauf une qui est plus lourde et qu'il faut
isoler en deux pesées. |
Il
se trouve que deux pesées est le minimum de pesées pour trouver une pièce
fausse parmi neuf et neuf est d'ailleurs le maximum. Une
pièce de plus et il faudra trois pesées. |
|
|
|
|||
|
Le
défi Parmi neuf billes visuellement identiques, une seule est légèrement
plus lourde. La retrouver en deux pesées. |
Le
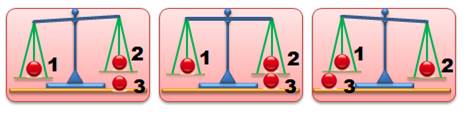
principe En une pesée, il est possible de discriminer
entre trois groupes de k billes du fait des trois mouvements possibles de la
balance:
Dans le cas de neuf billes, on formera trois
groupes de trois billes. |
||
|
Explications |
|||
|
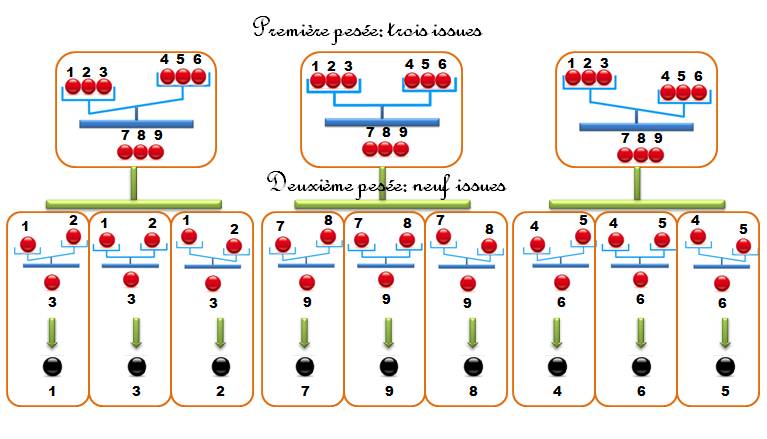
Première
pesée |
La bille lourde est parmi les billes 1, 2 et 3 |
||
|
Première
pesée |
La bille lourde est parmi les billes de 1 à 6 pèsent le même poids. La bille la plus lourde est parmi 7, 8 et 9. |
||
|
Première
pesée |
La bille lourde est parmi les billes 4, 5 et 6 |
||
|
Seconde pesée |
À l'issue de la première pesée, nous connaissons le groupe de trois
billes parmi lesquelles se trouve la bille lourde. La pesée permet de trouver laquelle est plus lourde. |
||
|
|
||||||||||||||
|
La
méthode vue ci-dessus marche pour toute quantité de billes jusqu'à 9 en deux
pesées. La
généralisation est possible avec les autres puissances de 3. Problème
des quatre-vingts billes Ainsi pour 80
billes, par exemple, il faudra quatre pesées en commençant avec trois
groupes de billes: 27, 27 et 26. |
Il est
possible de détecter une bille plus lourde
parmi k en n pesées:
|
|||||||||||||
Voir Puissances de 3
|
|
||
|
Solution
par dichotomie La
résolution est immédiate avec ce que nous avons vu. Pourquoi
8 et pas 9 ? Mystère En tout
cas, on utilise la tactique de groupement
en 3 + 3 + 2 = 8 |
Deux groupes de trois pièces
|
|
|
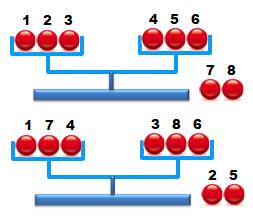
Solution
par combinaisons La
solution par combinaisons consiste, en utilisant le même groupement (3,3 ,2),
à faire deux pesées consécutives avec des combinaisons de billes différentes. La bille
fautive émergera selon les trois issues réalisées deux fois pour deux pesées,
soit 23 = 8 combinaisons Ça tombe
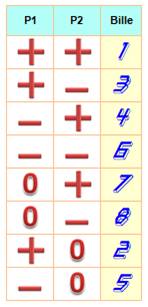
bien pour trouver une bille parmi huit Lecture
de la table des issues Ligne 1: si le plateau gauche descend lors de la
prière pesée et aussi lors de la seconde pesée, la bille 1 est la plus
lourde. Ligne 2: si le plateau gauche penche à droite
puis à gauche, la bille responsable est la 3. Etc. Ligne 8: si le plateau gauche descend et que la
seconde pèse donne l'équilibre, la bille 5 est la plus lourde. |
|
|
|
On trouve
sur Internet la question pour une bille plus lourde
(ou plus légère) pour 26 billes ou 80
billes ou …. Elles sont aussi faciles à résoudre que celle-ci. C'est une
autre histoire lorsque la bille est soit plus lourde,
soit plus légère, sans qu'on le sache a priori. >>> |
![]()
|
Retour |
|
|
|
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Voir
liste |
|
Cette
page |
![]()