|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mono: une bille est
plus lourde (ou plus légère) Ambi: une
bille est plus lourde ou plus légère
sans que nous le sachions a priori |
![]()
|
Énigme de la pesée impossible des DOUZE BILLES ou BALLES, BOULES, PIÈCES Méthode par combinaisons de pesées ou Méthode ternaire
Nous connaissons la méthode classique de résolution par dichotomie: pesées de plus en plus
réduites pour atteindre la balle intruse: pesée
4-3-2. La méthode par combinaison de pesées consiste à
effectuer trois pesées de deux fois quatre billes: pesée
4-4-4. Cette page propose cette
solution avec toutes les explications pour la bâtir. En prime, la liste des
884 solutions possibles. |
|
|
|||
|
Notation pour une pesée Pour une
pesée, il existe trois issues qui seront notées (– = +). D'où
l'idée d'utiliser une numération
ternaire. |
Gauche equilibre Droite –1 0 +1 |
||
|
Trois pesées Avec
trois pesées il existe 2 x 13 possibilités de mouvements des plateaux: soit
26 mouvements (ou issues de pesées). Ça tombe
bien: 1 bille peut être plus lourde ou plus légère parmi 12 billes; soit 24
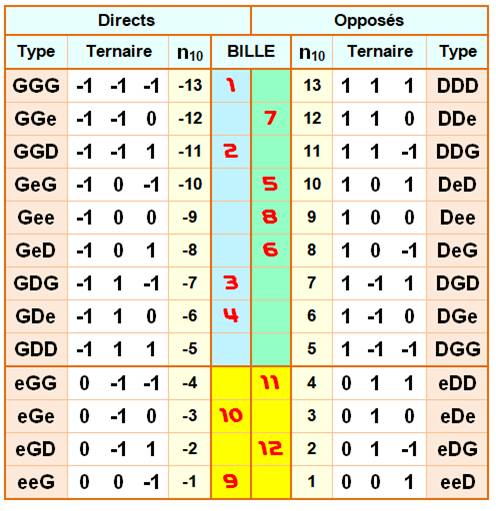
possibilités. Déductions Par exemple sur la première ligne du tableau à
laquelle on associe la bille n°1:
Le tableau indique également les nombres ternaires
associés et sa conversion décimale. Idée Comment combiner les billes sur les plateaux de
sorte que chaque possibilité de bille intruse provoque une suite d'issues
différentes ? Même s'il y a 24 possibilités pour 26 issues de
pesées, il existe quelques contraintes qui limitent les solutions. |
Tableau des issues de trois pesées
Voir Table des nombres
ternaires équilibrés Rappel: conversion du
nombre [1, 1, -1] en ternaire équilibré: 1x9 + 1x3 – 1x1 = 11 en base 10. |
||
|
|
||
|
Chaque
pesée comporte 4 billes à gauche, quatre billes à droite. Que
peut-on déduire de ces trois pesées?
Les huit
issues de pesées permettent d'identifier la bille lourde parmil les huit
billes. Très bien! Nous
avons compris le principe, mais maintenant il faut passer à douze billes. Les
cas où les plateaux sont en équilibre vont nous aider. |
|
|
|
|
|||
|
Quelles
sont les propriétés des ces trois pesées pour aboutir à une solution ? |
En fait, quelles sont les règles qui peuvent conduire
à un algorithme de recherche des solutions ? |
||
|
Règle 1 Toutes les billes sont impliquées dans chaque
pesée et une seule fois en trois groupes de quatre. |
On vérifiera que la somme sur
chaque ligne vaut 78: |
||
|
Règle 2 On place quatre billes à droite, quatre billes à
gauche et quatre billes de côté et on les numérote. |
Toute les solutions commencent par [1, 2, 3, 4] versus [5, 6,7, 8] et [9, 10, 11,
12] |
||
|
Règle 3 Une bille du plateau gauche est lourde si le
plateau gauche descend. Etc. |
Les quatre billes du plateau gauche sont sur les
lignes qui commencent par G (zone bleue) Les quatre billes du plateau droit sont sur les
lignes qui commencent par D (zone verte). Les quatre billes mise de côté sont sur les
lignes qui commencent par E (zone jaune). Bilan: 126 x 126 x 70 = 1 111 320 cas à explorer |
||
|
Règle 4 – Intervention de la
numérotation décimale Les chemins pour une bille est double: un chemin direct
pour identifier si elle est lourde et un chemin opposé pour identifier si
elle est légère. GDE (4) = chemin balle 4 pour lourde DGE (-4) =
chemin balle 4 pour légère |
Parmi les combinaisons, il faut exclure celle
pour lesquelles le chemin inverse est déjà affecté à une bille. Dit-autrement, si le chemin prend le numéro
décimal 4, on exclut le chemin numéroté -4 pour une autre bille. En logique: l'inverse d'un membre du plateau
droit n'est pas membre du plateau gauche. |
||
|
Règle 5 – Intervention de la
numérotation ternaire Chaque pesée doit respecter la répartition en
trois groupes de quatre. La première est acquise par construction. Le
chiffre de poids fort en ternaire est -9 pour gauche; +9 pour droite et 0
pour équilibre. La somme est nulle. |
Pour obtenir la bonne répartition lors de la
deuxième pesée, la somme des chiffres de poids intermédiaires (3) doit être
nulle. Comme elle doit être nulle pour le chiffre de
poids faible (1). Une sommation sur les chiffres du milieu pour tous
les numéros de billes sélectionnées fera l'affaire. idem pour le chiffre de
droite. |
||
|
|
||
|
L'implémentation de l'algorithme en programme montre qu'il y a 884
solutions au problème de la pesée des douze billes. Le tableau montre les six premières solutions. Voir Toutes les
solutions |
Tableau de l'affectation des
billes (rouge) à un nombre qui,
convertit en ternaire, donne l'issue de la pesée pour cette bille
|
|
|
Lecture de la table – Première
ligne: Affectation des billes à un numéro (à gauche)
et conversion ternaire pour établir
les trois pesées (à droite). Ex: la bille 1 est associée
à -1310 = [-1, -1, 1], soit trois pesés sur le plateau de gauche.
Pour la bille 2, on a -1210 = [-1, -1, 0], soit deux pesées à
gauche et, elle est mise de côté pour la troisième pesée.
Ligne 2 et ligne 3 du tableau
ci-dessus
Ligne 884 du tableau exhaustif
Voir Liste
exhaustive des 884 solution |
||
|
|
||
|
|
Commentaires Le package combinatoire est appelé (calcul des
combinaisons avec l'instruction choose). Le compteur de solution kt est initialisé. Trois listes (M, E et P) pour la liste des
possibilités en Moins, Égal ou Plus. Règle 3. Trois listes (MM, EE et PP) qui contiennent les
combinaisons de 4 parmi les nombres des listes originelles. Les variables en
q comptent la quantité de combinaisons pour chaque liste. Trois boucles pour associer chacune des
combinaisons (Mc, Ec et Pc) de chacune des trois listes. On vérifie que les membres en moins de Mc
(plateau de gauche) ne sont pas dans ceux de Pc (plateau de gauche). Règle 4 d'exclusivité. Pour les 12 valeurs retenues dans Mc, Ec et Pc,
conversion en ternaire équilibré (instruction ter de conversion ternaire
équilibré, à créer). Ti, T2 et T3 sont les sommes des chiffres de
poids foret, moyen et faible des 12 nombres ternaires On ne conserve que les cas où ces trois totaix
sont nuls. Règle 5. Ces valeurs retenues sont affichées (lprint). En fin de programme, on demande la valeur du
compteur kt. |
|
Voir Programmation – Index
![]()
|
Retour |
|
|
|
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Voir
liste
|
|
Cette
page |
![]()