NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/02/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Énigmes de Pesées
Débutants Général	BILLES							Glossaire Général
INDEX Jeux, énigmes	Débutants		Introduction		Dix Sacs		Six poids
	9 billes (mono)		4 billes (ambi)		Poids-étiquettes		Autres pesées
	12 par dichotomie (ambi)			12 par combinaisons (ambi)		12 billes (++)
		Sommaire de cette page >>> Pesée de 2 billes >>> Pesée de 3 billes >>> Pesée de n billes >>> Tactique

Mono: une bille est plus lourde (ou plus légère)

Ambi: une bille est plus lourde ou plus légère sans que nous le sachions a priori

Énigmes de pesée – Débutants
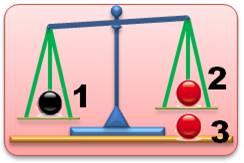
Il existe de nombreuses énigmes demandant de retrouver un intrus parmi une collection de billes (de balles, de boules de billards, de pièces de monnaie, de bagues, etc.). Certaines sont très simples et d'autres réputées insolubles ou très difficiles. Cette page est une introduction à ce type d'énigme et aux principes de leur résolution.	Les billes 1 et 2 sont plus lourdes que les billes 3 et 4.

Pesée de deux billes
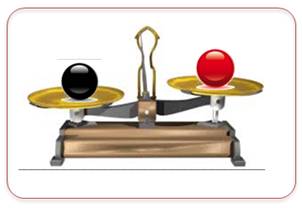
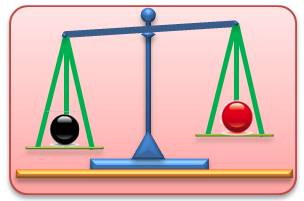
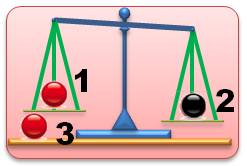
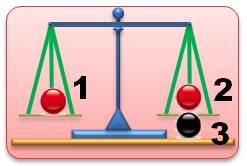
Disposant de deux billes, il s'agit de dire laquelle est la plus lourde. La pesée est effectuée avec une balance à deux plateaux. Qu'elle soit du type Roberval (en haut) ou trébuchet (en bas). La plus lourde est celle qui fait descendre le plateau. Ici, le plateau de gauche. C'est la bille noire qui est la plus lourde. Ou, autrement-dit, c'est la boule rouge qui est la plus légère. Note: dans toutes ces énigmes, la différence de poids est minime et, en tout cas, inférieure au pois d'une bille. Les pesées impliquent donc, la même quantité de billes sur chaque plateau.

Pesée de trois billes
Effet	Illustration	Notation
On nous présente trois billes identiques, sauf en poids. L'une est plus lourde que les deux autres. Il s'agit de trouver la plus lourde en une seule pesée. On effectue la pesée entre deux boules. Disons la 1 et la 2 et on laisse de côté la 3. Trois possibilités de mouvements des plateaux: Le plateau gauche descend: la bille 1 est la plus lourde; Le plateau droit descend: la bille 2 est la plus lourde; ou Les plateaux restent en équilibre et c'est la bille 3 qui est la plus lourde. Chaque pesée comporte trois issues de pesées. Avec les pesées, on compte par trois avec la notation classique {–1, 0, +1} du système ternaire.		Gauche +1
		Droite –1
		Équilibre

Pesée de n billes – Cas du problème des 80 billes
Prenons n = 80 billes. Comment s'y prendre? On compte par trois; alors, formons trois groupes de billes.	80 billes au total 27 billes sur le plateau gauche 27 billes sur le plateau droit 26 billes laissées de côté
La première pesée permet de détecter le groupe de billes dans lequel se trouve la bille la plus lourde. On reforme trois groupes.	27 ou 26 billes au total 9 billes sur le plateau gauche 9 billes sur le plateau droit 9 ou 8 billes laissées de côté
On effectue la pesée suivante selon le même principe pour arriver finalement et progressivement à la bille fautive.	9 ou 8 billes au total 3 billes sur le plateau gauche 3 billes sur le plateau droit 3 ou 2 billes laissées de côté
Cette méthode de raffinement progressif est dite méthode par dichotomie (ou trichotomie).	Problème général de n billes en k pesées

Suite pour ce type d'énigmes dont le représentant est l'énigme des neuf billes

Tactique de pesée
Avec n billes, comment constituer les trois groupes ?	Actions	Exemple 1	Exemple 1
	Prendre M, le multiple de 3 qui est juste plus grand que n.	n = 80 N = 81 = 3 x 27	n = 28 N = 30 = 3 x 10
	Formez deux groupes avec le premier sous-multiple de M.	27 et 27	10 et 10
	Le troisième groupe est formé avec ce qui reste.	80 – 2x27 = 26	28 – 2x10 = 8
Bilan	La première pesée s'effectue avec les deux premiers groupes en laissant le troisième de côté.	(27 =? 27) & 26	(10 =? 10) & 8

Retour	Pesée des quatre cubes
Suite	Énigme de pesées – Introduction Six poids avec étiquettes mélangées Quel est le poids des trois ?
Voir	Adam en douze heures Alexandrins longs et courts Arbre de Distribution Échecs Énigmes de transvasements Faire 12 avec cinq fois le même nombre Jeux – Index Jeux avec 10 Jeux de partage Les 12 travaux d'Hercule Pentaminos Sudoku Transfo Boulanger
DicoNombre	Nombre 3
Cette page	http://villemin.gerard.free.fr/aJeux1/Pesee/BallDebu.htm