NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/04/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PUISSANCES
Débutants Général	Puissances de n		Glossaire Puissance
INDEX Puissances des nombres	Puissance de 2	Puissance de 3
		Sommaire de cette page >>> Puissance de 3 – Valeurs >>> Derniers chiffres – Cycles >>> Puissance de 3 comme somme de puissance de k >>> Programmation Maple

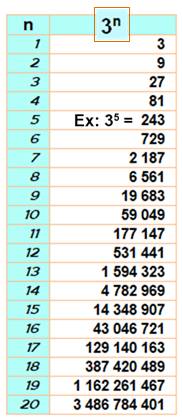
PUISSANCE de 3

Valeurs et propriétés des derniers chiffres.

PUISSANCE de 3
Exemples 3 x 3 = 3^2 = 9 3 x 3 x 3 = 3^3 = 27 3 x 3 x 3 x 3 = 3^4 = 81 Cycle 3^21 = 10460353203 Les deux derniers chiffres reprennent la valeur de 3^1. Chaque fois que n augmente de 20, on retrouve les mêmes deux derniers chiffres.

Merci à Cédric de L'île logique

Derniers chiffres – Cycles
Chiffre des unités: Longueur du cycle: 4	3, 9, 7, 1
Deux derniers chiffres: Longueur du cycle: 20 à partir de 3	3, 9, 27, 81, 43, 29, 87, 61, 83, 49, 47, 41, 23, 69, 7, 21, 63, 89, 67, 1
Trois derniers chiffres: Longueur du cycle: 100 à partir de 3 Il existe un cycle pour les m derniers chiffres. La longueur augmente rapidement. Voir Le cas des puissances de 2	3, 9, 27, 81, 243, 729, 187, 561, 683, 49, 147, 441, 323, 969, 907, 721, 163, 489, 467, 401, 203, 609, 827, 481, 443, 329, 987, 961, 883, 649, 947, 841, 523, 569, 707, 121, 363, 89, 267, 801, 403, 209, 627, 881, 643, 929, 787, 361, 83, 249, 747, 241, 723, 169, 507, 521, 563, 689, 67, 201, 603, 809, 427, 281, 843, 529, 587, 761, 283, 849, 547, 641, 923, 769, 307, 921, 763, 289, 867, 601, 803, 409, 227, 681, 43, 129, 387, 161, 483, 449, 347, 41, 123, 369, 107, 321, 963, 889, 667, 1

Voir Programmation de cette recherche / Puissances de 3 en ….00001

Puissance de 3 comme somme de puissance de k distinctes

Exemple: 3⁴ = 81 = 2⁰ + 2⁴ + 2⁶ = 1 + 16 + 64

Les puissances impliquées sont toute différentes.

Liste:

n, 3ⁿ [termes de la somme en puissances de 2]
1, 3, [1, 2]

2, 9, [1, 8]

3, 27, [1, 2, 8, 16]

4, 81, [1, 16, 64]

5, 243, [1, 2, 16, 32, 64, 128]

6, 729, [1, 8, 16, 64, 128, 512]

7, 2187, [1, 2, 8, 128, 2048]

8, 6561, [1, 32, 128, 256, 2048, 4096]

9, 19683, [1, 2, 32, 64, 128, 1024, 2048, 16384]

10, 59049, [1, 8, 32, 128, 512, 1024, 8192, 16384, 32768]

…

Voir Cas des puissances de 2

Programmation Maple
	Programme qui cherche les partitions des cubes en puissances de 2. Commentaires La première partie consiste créer la liste de toutes les possibilités de combinaisons des puissances de 2 en Q. On crée d'abord la liste désirée des puissances de 2 en A. On l'imprime pour apprécier la valeur maximale. Elle doit être suffisante. La seconde partie réalise la somme de chacune des combinaisons et compare cette valeur au nombre n = les cubes successifs. Si le cube vaut la somme de puissances de 2, on l'imprime. Résultats du traitement en bleu.

Voir Programmation – Index

Suite	Puissance 2 – Propriétés Puissance des nombres – Autres pages
Voir	Puissances – Index Puissances et exposants
DicoNombre	Nombre 3
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Puiss3.htm