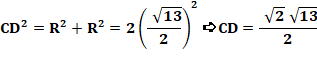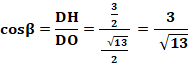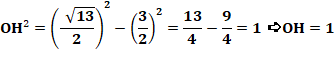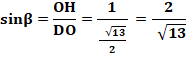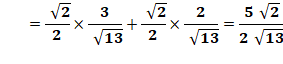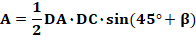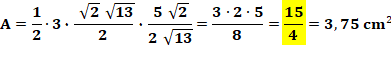Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 18/03/2024 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX – Défis	Angles et cercle	Double triangle rectangle
	Nappe sur table	Triangle rectangle partagé	Rectangle et triangle
	Triangle dans le cercle	Carré et triangle équil.	Triangles dans triangle
	Triangle dans quadrilatère	Trapèze et triangle	Trois triangles réunis

Triangle dans un quadrilatère Calculer l'aire Un triangle formé à partir de trois sommets d'un quadrilatère dont deux sommets opposés sont droits. Calculer l'aire de ce triangle. Pas si simple …
	Sommaire de cette page >>> Le triangle dans le quadrilatère	Débutants Géométrie Glossaire Géométrie

Triangle dans quadrilatère		haut
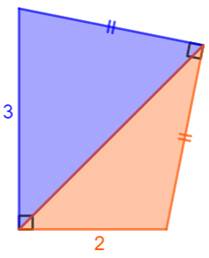
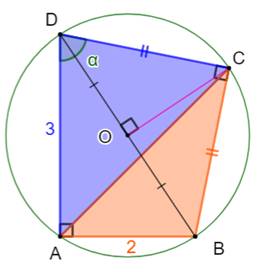
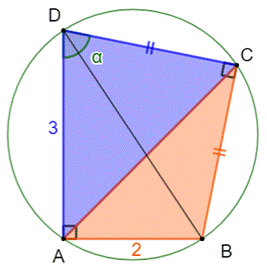
Construction Un quadrilatère dont deux angles opposés sont droits. Les côtés d'un angle droit sont de même mesure (égaux). Les deux autres côtés mesurent 2 cm et 3 cm. Calculer l'aire du triangle bleu ? Pistes Avec deux angles droits opposés, le quadrilatère ABCD est inscriptible dans un cercle dont BD est un des diamètres. En effet, l'angle droit BAD intercepte un diamètre comme le fait l'angle BCD. Idée: calculer l'aire du triangle ACD avec la formule du sinus: A = ½ AD٠CD٠ sinα Peut-on calculer la longueur CD et la valeur de l'angle alpha ?
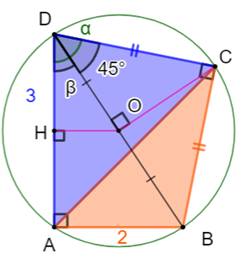
Calcul de CD Soit O, le centre du cercle circonscrit. OB, OC et OD sont des rayons ( = R). Dans le triangle isocèle rectangle BCD, les angles à la base valent 45°. Le segment OC qui est porté par la médiane, est aussi la médiatrice de la base BD. L'angle en O est droit. Dans le triangle rectangle OCD: Angle bêta Le segment OH est sur la perpendiculaire en O à AD. Dans le triangle rectangle DHO, on connait DO = R et DH = 3/2. 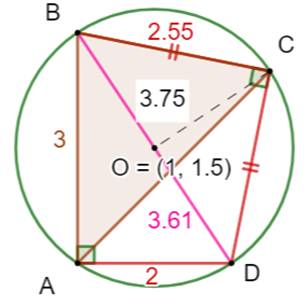Sinus de l'angle en D Aire du triangle ACD	Aire ACD = 3,75 cm² Aire ABC = 2, 5 cm² Angle alpha = 78,69 …° BC = CD = 2,54951 … cm

Voir Sinus et cosinus / Addition des angles

Illustration avec GeoGebra

Haut de page

Retour	Voir haut de page Défis en algèbre et en géométrie – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Site	Find the blue shaded area – Math Olympiad – Math Booster
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/TrgQuadr.htm