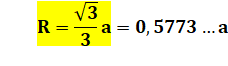Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 25/01/2025 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Carré et cercle	Deux demi-cercles
	Coin du carré replié	Quatre cercles et carré	Demi-cercle et rectangle
	Quatre carrés	Carré et triangle équil.	Carré et 2 demi-cercles
	Carré oblique	Trois carrés plus un	Cercle et oblique
	Rectangle et deux cercles

Carré, Cercle et Oblique
	Sommaire de cette page >>> Cercle et oblique dans carré	Débutants Géométrie Glossaire Géométrie

Cercle et oblique dans carré		haut
Problème assez classique utilisant la propriété des tangentes et la loi des cosinus.
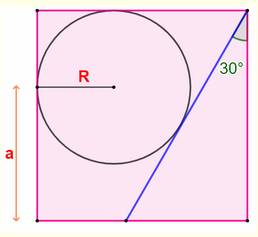
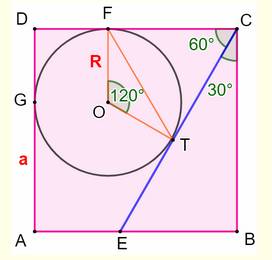
Construction Dans un carré, on trace une oblique à 30°. Dans l’espace libre, on inscrit un cercle de rayon R. Calculer la valeur du rayon du cercle en fonction de la distance a. Pistes Le centre O du cercle est à égale distance des côtés du carré (point de tangence) : OF = OG = R et le quadrilatère DFOG est un carré de côté R. Avec DG = DF, on a AG = FC = a L’angle FCT est le complémentaire de 30°, soit 60°. Les segments CF et CT sont des segments de tangentes issues du point C : ils ont la même longueur. Même longueur et angle de 60° entrainent que le triangle CFT est équilatéral : FT = FC = CT = AG = a Triangle OFT Avec OF = OT = R, le triangle OFT est isocèle d’angle au sommet 120° (les angles à la base valent 90° – 60° = 30°). On connaît la longueur de la base FT = a. La loi des cosinus permet d’écrire : FT² = OT² + OF² – 2·OT·OF cos 120° a² = 2R² – 2R² (- 1/2) a² = 3R²	Figure Figure avec notations

Haut de page

Retour	Défis en géométrie – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Carré dans le cercle Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CarreObl.htm