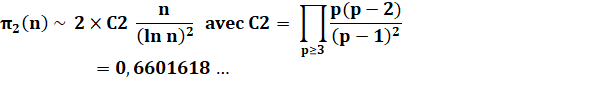|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
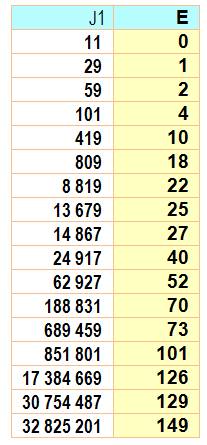
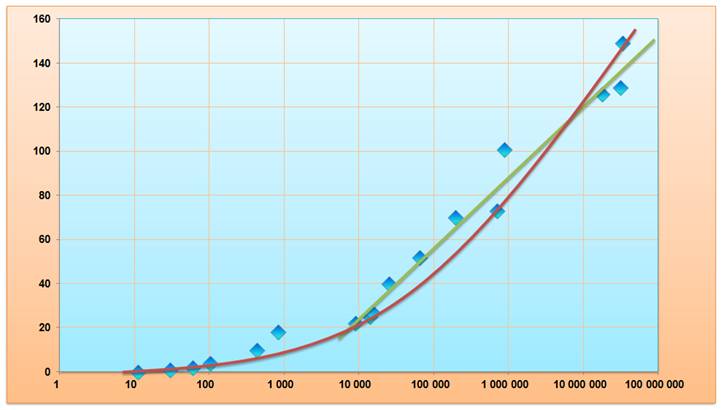
Quantités et PREMIERS JUMEAUX Combien
de nombres premiers entre les paires de jumeaux ? Combien de jumeaux inférieurs à un nombre n donné ? |
|
|
|
|
2
3 5 7
11 13 17
19 23 29
31 37 41
43 47 53 59 61 67 71 73 79
83 89 97 101 103
Leur étude cherche à modéliser la répartition des
nombres jumeaux et à tenter de prédire quel est l'ordre de grandeur du nième
couple de jumeau.
Conjecture sur la
quantité de couples de jumeaux
C2 est la constante de Shah et Wilson ou la
constante des premiers jumeaux et de Goldbach (twin prime and Goldbach
constant). Voir Efficacité de cette formule / Constante de Brun Voir OEIS A005597 – Decimal expansion of the
twin prime constant C2 Qui indique cette valeur: C2 = 6601618158 4686957392 7812110014
5557784326 2336028473 3413319448 4233354056 4230449527 7143760031 4138398679 11779 …
|
|
Premier
simple en anglais: isolated prime
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Valeurs Graphe
|
|
|
|
||
|
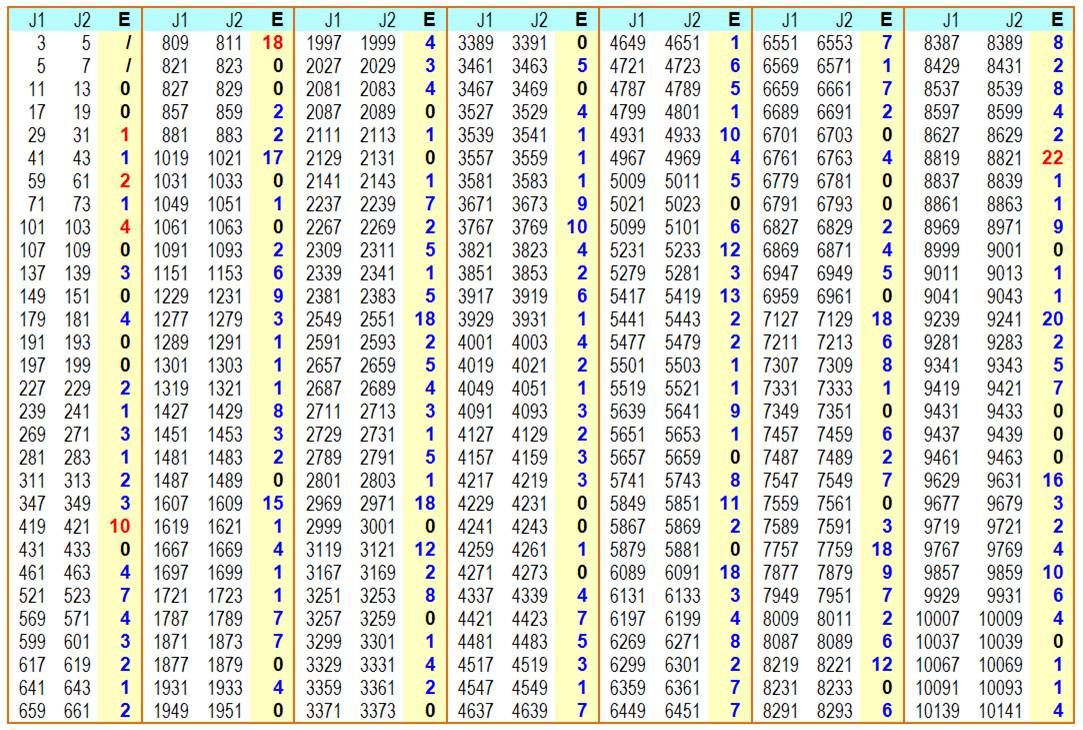
Quantité
de jumeaux dans la centaine indiquée. Ex: 8 paires da 0 à 99 2 paires de 300 à 399 qui sont: 311/313 et
347/349 Centaines sans jumeaux 700, 900, 1500, 2400, 3000, 4800, 5100, 5300, 5900,
7000, 7600, 8100, 8700, 9100, 9500 |
[0, 8], [100, 7], [200, 4], [300, 2], [400, 3],
[500, 2], [600, 3], [700, 0], [800, 5], [900, 0], [1000, 5], [1100, 1],
[1200, 3], [1300, 2], [1400, 4], [1500, 0], [1600, 4], [1700, 2], [1800, 2],
[1900, 3], [2000, 3], [2100, 3], [2200, 2], [2300, 3], [2400, 0], [2500, 2],
[2600, 2], [2700, 3], [2800, 1], [2900, 1], [3000, 0], [3100, 2], [3200, 2],
[3300, 4], [3400, 2], [3500, 4], [3600, 1], [3700, 1], [3800, 2], [3900, 2],
[4000, 4], [4100, 2], [4200, 5], [4300, 1], [4400, 2], [4500, 2], [4600, 2],
[4700, 2], [4800, 0], [4900, 2], [5000, 2], [5100, 0], [5200, 2], [5300, 0],
[5400, 3], [5500, 2], [5600, 3], [5700, 1], [5800, 3], [5900, 0], [6000, 1],
[6100, 2], [6200, 1], [6300, 1], [6400, 1], [6500, 2], [6600, 2], [6700, 4],
[6800, 2], [6900, 2], [7000, 0], [7100, 1], [7200, 1], [7300, 3], [7400, 2],
[7500, 3], [7600, 0], [7700, 1], [7800, 1], [7900, 1], [8000, 2], [8100, 0],
[8200, 3], [8300, 1], [8400, 1], [8500, 2], [8600, 1], [8700, 0], [8800, 3],
[8900, 1], [9000, 2], [9100, 0], [9200, 2], [9300, 1], [9400, 4], [9500, 0],
[9600, 2], [9700, 2], [9800, 1], [9900, 1], [10000, 4] |
|
|
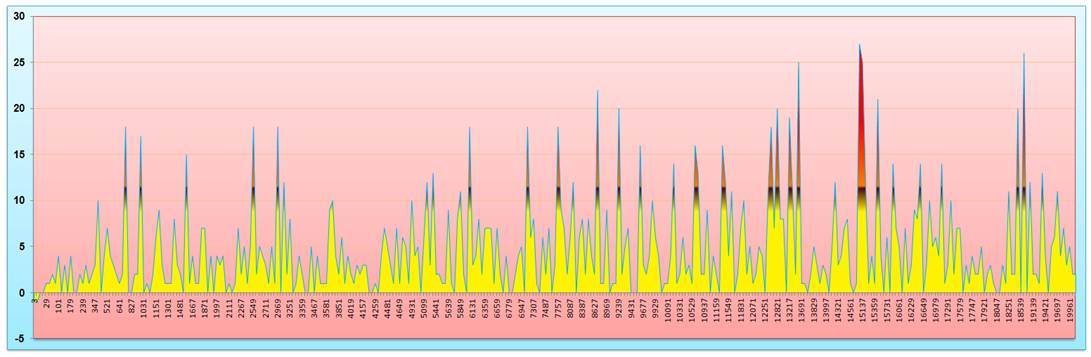
Quantité
dans le millier indiqué. Aucune
sans jumeaux. |
[0, 35], [1000, 26],
[2000, 20], [3000, 21], [4000, 23], [5000, 17], [6000, 19], [7000, 13],
[8000, 14], [9000, 15], [10000, 16], [11000, 14], [12000, 11], [13000, 15],
[14000, 11], [15000, 12], [16000, 13], [17000, 18], [18000, 12], [19000, 15],
[20000, 15], [21000, 15], [22000, 16], [23000, 14], [24000, 6], [25000, 12],
[26000, 11], [27000, 15], [28000, 12], [29000, 9], [30000, 11], [31000, 13],
[32000, 19], [33000, 13], [34000, 16], [35000, 11], [36000, 9], [37000, 12],
[38000, 11], [39000, 9], [40000, 8], [41000, 12], [42000, 12], [43000, 11],
[44000, 11], [45000, 7], [46000, 12], [47000, 11], [48000, 13], [49000, 17],
[50000, 9], [51000, 14], [52000, 8], [53000, 11], [54000, 8], [55000, 11],
[56000, 14], [57000, 9], [58000, 11], [59000, 11], [60000, 10], [61000, 6], [62000, 8], [63000, 10], [64000, 9], [65000,
14], [66000, 6], [67000, 10], [68000, 9],
[69000, 12], [70000, 16], [71000, 10], [72000, 11], [73000, 6], [74000, 10], [75000, 9], [76000, 11], [77000,
9], [78000, 9], [79000, 11], [80000, 13], [81000, 12], [82000, 13], [83000,
8], [84000, 12], [85000, 11], [86000, 8], [87000, 14], [88000, 10], [89000,
8], [90000, 10], [91000, 10], [92000, 12], [93000, 12], [94000, 13], [95000,
8], [96000, 7], [97000, 15], [98000, 13], [99000, 8], [100000, 6] |
|
Page créée suite à une impulsion donnée par Olivier Damide
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()