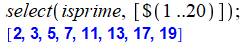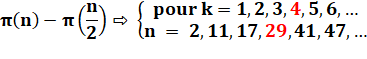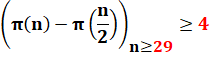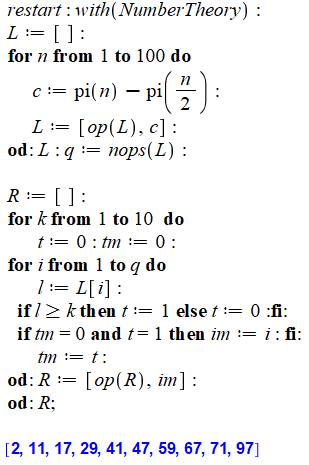type de nombres: nombres premiers de Ramanujan

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/03/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Premiers	NOMBRES PREMIERS				Glossaire Premiers
INDEX Types de premiers Premiers Nombres		Premiers	Presque Premiers		Probablement P.
		Premiers équilibrés	Premiers forts		Cube (cuban)
		Premiers bons	Premiers inévitables		Primeval
		Premiers de Ramanujan		Premiers de Bertrand
		Sommaire de cette page >>> Approche >>> Définition et historique >>> Propriétés >>> Liste des nombres premiers de Ramanujan >>> Programmation Maple

NOMBRES PREMIERS de RAMANUJAN

Sorte de statistiques sur la quantité de nombres premiers par tranches de nombres.

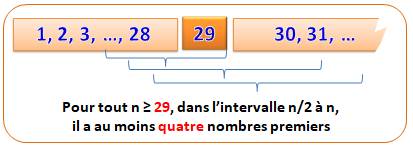
Nombre premier tel que la quantité de nombres premiers comprise entre n et n/2 soit égale à un nombre k donné.

À partir du nombre 29, la quantité de nombres premiers dans la seconde moitié des nombres de 1 à n est supérieure à trois.

Anglais: Ramanujan primes

Approche
Jusqu'à n = 20, il y a huit nombres premiers et quatre de 10 à 20 (seconde moitié). On s'intéresse à ce cas où k = 4 nombres premiers compris entre n et n/2. On note Pi(n) la fonction qui indique la quantité de nombres premiers jusqu'à n.	Nombre premier jusqu'à n = 20 2, 3, 5, 7, 11, 13, 17, 19 Pi (20 ) = 8 Pi (10, 20) = 4 Note: liste des premiers avec Maple
En fait, on cherche le nombre n le plus petit tel que tous les nombres premiers plus grands présentent au moins k nombres premiers dans la seconde moitié des nombres. Dans la liste ci-contre, on marque en rouge les cas où k est 4 ou plus. À partir le 29^e, on a k = 4 ou plus. Le nombre 29 est un nombre premier de Ramanujan.	Quantité de premiers dans la seconde moitié pour n de 1 à 40 0, 1, 2, 1, 2, 1, 2, 2, 2, 1, 2, 2, 3, 2, 2, 2, 3, 3, 4, 4, 4, 3, 4, 4, 4, 3, 3, 3, 4, 4, 5, 5, 5, 4, 4, 4, 5, 4, 4 …

Définition et historique
Avec Pi (n) = quantité k de nombres premiers entre 1 et n et Pi (n/2), celle entre 1 et n/2. La quantité k de nombres premiers dans la seconde moitié de l'intervalle jusqu'à n est bornée inférieurement. Cette borne inférieure est le nombre premier de Ramanujan de rang k. Du fait de la condition "minimum", ce nombre est automatiquement un nombre premier.	Formulation Exemple À partir de n = 29, on trouvera toujours quatre nombres premiers, au moins, dans la seconde moitié des nombres de 1 à n. Alors R(4) = 29.
Postulat de Bertrand (1845) Démontré par Tchebychev (1852), démonstration plus simple par Ramanujan (1919) puis par Paul Erdös (1932) À l'occasion de cette démonstration, Ramanujan publia le résultat figurant sur cette page.		Postulat de Bertrand ou Théorème de Tchebychev Entre n et 2n, il existe toujours un nombre premier. C'est un cas particulier pour k = 2 du calcul des nombres premiers de Ramanujan.

Anglais (d'après Jonathan Sondow)

Propriétés
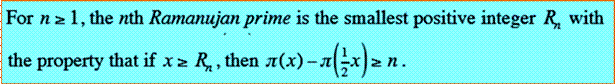
Un nombre de Ramanujan de rang k est situé entre les premiers de rangs 2k et 3k. En 2011, Sondow, Nicholson, and Noe ont démontré que R(k) ≤ 41/47 P(3k).	Exemple R(4) = 29 compris entre P(8) et P(12): 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47
Un nombre de Ramanujan de rang k est situé entre ces deux valeurs en logarithmes.	Exemple R(4) = 29 compris 8 ln(8) = 16, 63… et 16 ln(16) = 44,36…
Pour k très grand (tendant vers l'infini). La convergence est très lente comme le montrent les exemples. Cette propriété est directement déduite du théorème des nombres premiers.	Exemple R(4) = 29 et 8 ln(4) = 11,09… R(99) = 1 429 et 198 ln(99) = 909,83…
Approximation de R(k) pour k de 1 à 1000.	Avec k = 2,216 Exemple R(4) = 29 et calcul: 28 R(99) = 1 429 et calcul: 1 402
Jusqu'à n = 19 000	46% des nombres premiers sont aussi Ramanujan.

Liste des nombres premiers de Ramanujan

Lecture

k = 04, R = 29

k = 21, R = 233

À partir du nombre 233, toutes les secondes moitiés des nombres comprennent au moins 21 nombres premiers.

Programmation Maple
		Commentaire Retourne la liste des nombres premiers de Ramanujan jusqu'à n (ici n = 100). Réinitialisation générale et appel aux logiciels de théorie des nombres pour le calcul de la fonction Pi(n). Déclaration de la liste L qui recevra Pi(n) – Pi(n/2). Première boucle de remplissage de la liste L pour n de 1 à 100. Déclaration de la liste R qui recevra les premiers de Ramanujan pour k de 1 à 10. Les indicateurs t et tm servent à mémoriser le passage à la valeur k ou plus dans la liste L. Pour chaque valeur de k, exploration de la liste L. L'indicateur t crée un "signal' qui vaut 1 chaque fois que k est au moins 4. L'indicateur tm garde la mémoire du t précédent. Si on conserve t = 1 sans jamais revoir de tm à 0, alors la valeur de i (équivalente à n) est placée dans R. En bleu, la liste établie selon k de 1 à 10.
	Avec ce programme, il est facile d'établir toute autre statistique. Ici avec la quantité de nombres premiers dans le dernier tiers, puis le dernier décile. Nombre premiers généralisés de Ramanujan dit k-premiers de Ramanujan.

Voir Programmation – Index / Programmation de cette recherche en Python, Java, C++ et C# par GeeksforGeeks

Suite	Voir haut de page Repunit Nombres premiers tronquables Nombres premiers effaçables Primeval
Voir	Tables de nombres – Index Types de premiers – Index Premiers – Index Place de ces nombres parmi les autres premiers Écarts entre nombres premiers – Index Jumeaux, cousins, constellations – Index
DicoNombre	Accès aux nombres cités sur cette page
Sites	Ramanujan Prime – Wolfram MathWorld OEIS A104272 – Ramanujan primes R_n: a(n) is the smallest number such that if x >= a(n), then pi(x) - pi(x/2) >= n, where pi(x) is the number of primes <= x OEIS A162996 - a(n) = Round(kn * (log(kn)+1)), with k = 2.216 as an approximation of R_n = n-th Ramanujan prime OEIS A164952 – Nombre 3-premier de Ramanujan, en considérant le dernier tiers Ramanujan Primes and Bertrand's Postulate par Jonathan Sondow Ramanujan primes – OEIS – Toutes les suites se rapportant à ce sujet
Cette page	http://villemin.gerard.free.fr/aNombre/TYPMULTI/PremRama.htm