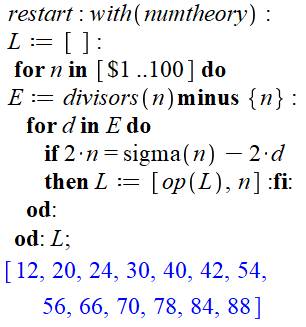Nombres admirables

Édition du: 11/12/2020

INDEX Nombres et division Types de nombres	Types de Nombres – Diviseurs
	Parfaits	Semi-parfaits (SP)	SP Primitifs	SP Primaires
	Refactorisables	Pratiques	Abondant primitifs	Giuga
	Facteurs-Diviseurs	Sigma / rad² = N	S-Parfaits	Admirables
	Balancés			Zumkeller

NOMBRES ADMIRABLES

& Nombres compatibles

Nombres cousins des nombres parfaits. Relation avec diviseurs et somme des diviseurs.

Nombre tel qu'il est égal à la somme de ses diviseurs dont un est retranché (la somme des diviseurs propres dont un avec signe négatif).
Ex: 12 = 1 – 2 + 3 + 4 + 6.

Concept développé par Jerome Michael Sachs (1914-2012).

Sommaire de cette page

>>> Définition

>>> Liste

>>> Programmation

>>> Nombres compatibles

Débutants

Nombres

Glossaire

Nombres

Définition			haut
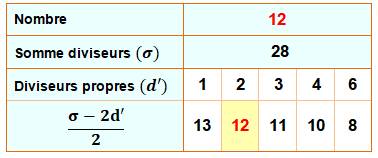
Nombre n tel que la somme de ses diviseurs diminuée du double de l'un des diviseurs propres est égale à deux fois le nombre n. Exemple Avec 12, ses diviseurs sont [1, 2, 3, 6, 12], la somme vaut 28 et les diviseurs propres sont [1, 2, 3, 6]. Pour le diviseur 2, la 28 – 2 x 2 = 24 = 2 x 12, c'est un nombre admirable.		Le nombre 12 est admirable
Formulation
Propriétés	Ils sont tous abondants et en nombre infini. Le plus grand nombre qui n'est pas somme de nombres admirables est 1 003. Si l'on admet un diviseur négatif dans la somme, peut-on en autoriser plusieurs ? Sachs, le père de ces nombres, l'envisageait.
Carré magique admirable Voir Carré magique

Liste

haut

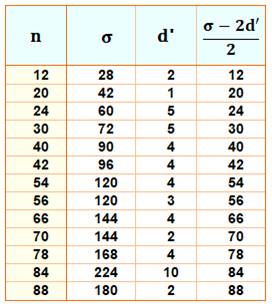
Nombres admirables jusqu'à 100 avec identification du diviseur qui engendre la propriété, ci-contre.

Liste jusqu'à 1100

12, 20, 24, 30, 40, 42, 54, 56, 66, 70, 78, 84, 88, 102, 104, 114, 120, 138, 140, 174, 186, 222, 224, 234, 246, 258, 270, 282, 308, 318, 354, 364, 366, 368, 402, 426, 438, 464, 474, 476, 498, 532, 534, 582, 606, 618, 642, 644, 650, 654, 672, 678, 762, 786, 812, 822, 834, 836, 868, 894, 906, 942, 945, 978, 992, 1002, 1036, 1038, 1074, 1086 …

Programme Maple		haut
Programme classique	Commentaires Réinitialisation et appel des logiciels de théorie des nombres. Déclaration d'une liste L qui accueillera les nombres admirables. Première boucle d'analyse des nombres n Liste des diviseurs en E. Deuxième boucle d'analyse des diviseurs. Examen de la relation "admirable". Si satisfairte, mettre n dans la liste des admirables. En bleu, résultat du traitement.
Programme avancé	Commentaires Mise en place d'une procédure qui retourne vrai si le nombre proposé est admirable. L'ensemble des diviseurs propres est obtenu à partir de celui des diviseurs auquel on retire (minus) le nombre lui-même Test le l'expression "admirable", mise à un de l'indicateur T et arrêt (break) de la recherche pour ce nombre. Le programme principale sélectionne les nombres admirable dans la liste 1 à 75 et en forme la liste.

Voir Programmation – Index

Nombres compatibles

haut

Les nombres amiables sont tels que l'un est la somme des diviseurs de l'autre.

Les nombres compatibles sont tels que l'un est égal à la somme admirable de l'autre. Notion introduite par Sachs.

Exemple

Diviseurs propres de 30: [1, 2, 3, 5, 6, 10, 15]

Somme admirable: – 1 + 2 + 3 + 5 + 6 + 10 + 15 = 40

Diviseurs propres de 40: [1, 2, 4, 5, 8, 10, 20]

Somme admirable: 1 + 2 + 4 + 5 + 8 – 10 + 20 = 30

Liste (premier nombre de la paire)

24, 30, 40, 42, 48, 60, 80, 80, 96, 102, 126, 140, 140, 156, 156, 156, 174, 180, 180, 198, 216, 224, 224, 264, 276, 280, 294, 294, 300, 320, 340, 372, 380, 384, 440, 440, 468, 500, …

Haut de page

Retour	Nombres parfaits
Suite	Nombre S-Parfait / Nombre de Zumkeller
Voir	Liens en haut de page
Sites	Admirable numbers – Numbers aplenty OEIS A111592 - Admirable numbers. A number n is admirable if there exists a proper divisor d' of n such that sigma(n)-2d'=2n, where sigma(n) is the sum of all divisors of n OEIS A109797 – First of a pair of compatible numbers, where two numbers m and n are compatible if sigma(n)-2dn=sigma(m)-2dm=m+n, for some proper divisors dn and dm of m and n respectively
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Admirabl.htm