|
||||||||||||||||||||||||||||||||
![]()
|
Couronnes magiques Carrés magiques creux Carrés
magiques dont on a supprimé la zone centrale. |
Anglais: Magic annulus / Hollow magic square
|
|
||||
|
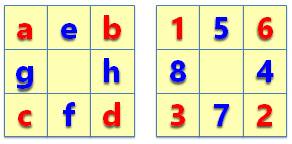
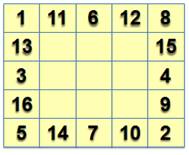
Défi Un carré
magique 3x3 sans le carré central. Remplir
avec les nombres de 1 à 8 tel que les quatre sommes lignes et colonnes soient
égales. Exemple 1 + 5 + 6 = 1 + 8 + 3 6 + 4 + 2 = 3 + 7 + 2 = 12 = m |
Générique et exemple
|
|||
|
Notations |
|
|||
|
Avec les médians |
S = 1 + 2 + 3 + 4 + 5 + 6 + 8 = 36 S = 36 = 2m + e + f S = 36 = 2m + g + h
e + f = g + h = t |
|
||
|
Sommes |
S = 36 = 2m + t 2S = 2 x 36 + 4m + 2t S = 36 =
s + 2t S = 36 = 4m – s |
s = 4 (m – 9) s est donc divisible par 4. |
||
|
Min Max |
smin
= 1 + 2 + 3 + 4 = 10 smax
= 5 + 6 + 7 + 8 = 26 La somme des coins peut prendre les valeurs de 10
à 26. Or, s est divisible par 4. Soit les valeurs
possibles de s et, par calcul les valeurs possibles de m et de t. |
s = (12, 16, 20, 24) m = (12, 13, 14, 15) t = (12, 10, 8, 6) |
||
|
Possibilités pour t |
t = e + f
= g + h = (12, 10, 8, 6) Avec les possibilités énoncées, il y a |
12 = 4 + 8 = 5 + 7 10 = 1 + 9 = 2 + 8 = 3 + 7 8 = 1 + 7 = 2 + 6 =
3 + 5 6 = 1 + 5 = 2 + 4 |
||
|
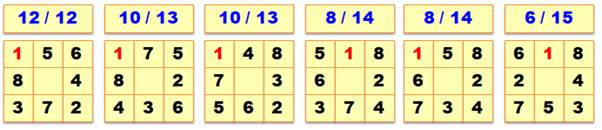
Les six solutions |
En testant les 8 couples 6 sont compatibles avec
la formation de la couronne magique. En haut de la solution, la valeur de t qui est
retenue et la valeur de la constante magique.
Avec symétries et rotations, il y a 48 solutions. |
|||
|
|
||
|
Grilles 2x2 et 4x4 Aucune solution avec une grille 2x2. C'est le cas aussi avec une grille 4x4. Dans ce cas, avec les mêmes notations, on a Somme des nombres de 1 à 12 = 6 x 13 = 78, et 78
= 4m – s Or 78 = 4 x
19,5 n'est pas divisible par 4. |
|
|
|
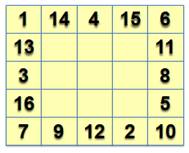
Grille 5x5 Avec une grille 5x5,
la somme des nombres de 1 à 16 vaut 8 x17 = 136, divisible par 4. La couronne
magique 6x6 devrait avoir des solutions. La somme des coins "s" prendre des
valeurs entre: 1+2+3+4 = 10 et 9+10+11+12 = 42. Celle des médians "t" peut varier
entre: 1+2+3+4+5+6 = 21 et 16+15+14+13+12+11= 81. Plages compatibles. Nombreuses solutions. Exemples t = 60 = 3 + 4 + 9 + 13 + 15 + 16 = 6 + 7 + 10 + 11 + 12 + 14 => m = 38
et s = 16 L'ordre des médians sur chaque ligne ou colonne
est indifférent. Paramètres du second exemple: m = 40; s = 24 et t = 56 La recherche d'autres solutions peut se faire
avec le tableur en fixant les trois paramètres et en procédant par
approximations successives. |
136 = 4m – s s = (10 à 42) => m = (36 à 44) 136 = 2m + t t = (21 à 81) =>
m = (57 à 27) Exemples
|
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaCMag/Couronne.htm
|
![]()