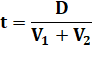|
|||||||||||||||||||||||||||||||||||||
![]()
Astuce
|
Un gars en mobylette
est dans la forêt, il est à sa vitesse maximale de 40km/h. Il avise qu'un feu
le poursuit par derrière à 60 km/h. Il sera vite rattrapé et cuit! Que faire? Il descend de
mobylette et allume un feu devant lui. Bonne astuce, même si
peu écologique: faire un feu en avant pour ne pas être rattrapé par le feu en
arrière. En effet, le feu va
partir devant lui à 60km/h et lui laissera la possibilité de passer
tranquillement sur les zones brûlées, tandis que le feu arrière va stopper
net lorsqu'il va atteindre la zone déjà brûlée par le feu allumé par le mec
en mob. |
Voir
Pensées
& humour
|
|
|
|
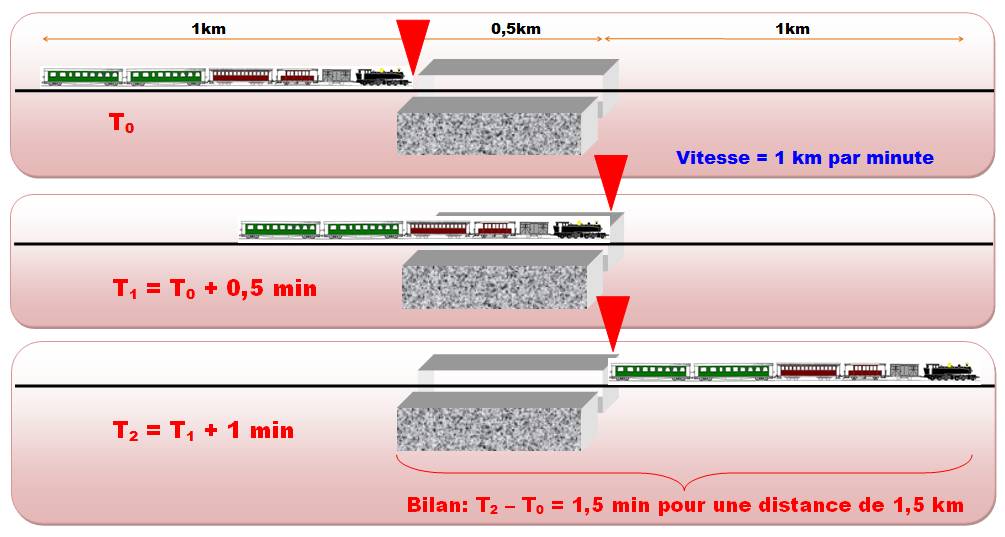
Problème Une gare dont le quai est long de 500 mètres. Un train long de 1
kilomètre file à 60 km/h. Combien de temps mettra-t-il à traverser le quai? Solution Dès l'annonce des données, je réalise que le train
parcourt 60 km en 1 h, soit, en divisant tout par 60, 1 km en 1 minute. Plusieurs étapes: T0 : l'avant du train est
en face du début du quai; T1 : l'avant du train est
en face de la fin du quai. L'avant a avancé de la longueur du quai soit un
demi-kilomètre. Il a mis une demi-minute pour le faire. T2 : l'arrière du train
arrive en face de la fin du quai après une minute. Bilan Pour passer la tête puis la queue
devant le quai, le train mettra 1,5 minute. Notes: pas de
"s" à minute tant qu'il n'y en a pas deux. Minute est abrégé en min. et non en mn. |
|
Illustration
Le
train sur l'illustration est le Train
des Pignes (qui sillonne l'arrière pays de la Côte d'azur)
|
Le
viaduc ferroviaire est visible de l'autoroute. Sa longueur est estimée à 3
km. Le TGV débouche à 320 km/h. Son double attelage l'amène à une longueur de
400 m. Pendant combien de temps le train sera-t-il en visibilité sur le pont? Longueur
du viaduc + longueur du train: 3,4 km Vitesse
du train: 60 minutes pour 320 km Temps
de parcours: X minutes pour 3,4 km Règle de trois (ou produit en croix ou
quatrième proportionnelle)
On fait toujours un
calcul de tête pour vérifier l'ordre de grandeur. Si le train
allait à 360km/h, ce serait 6 km en une minute. Pour les 3km du viaduc, nous aurions
0,5 minute. Oui, avec 0,6 min l'ordre de grandeur est respecté. |
|
|
|
|
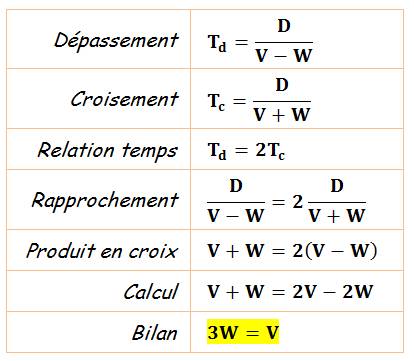
Problème avec deux trains Deux
trains avancent, chacun à sa vitesse constante. Deux
cas se présentent:
Il
leur faut deux fois plus de temps pour se dépasser que pour se croiser. Quelle
le rapport des vitesses entre les deux trains. Réponse Dans
chaque cas la distance à franchir est D (= somme des deux longueurs de
trains). Avec
V et W les vitesses des trains
Un
des trains avance trois fois plus vite que l'autre. |
|
Devinette des deux
trains
|
L'un
va à la rencontre de l'autre à 120 km/h pour l'un et à 140km/h pour l'autre.
Quelle distance les séparent une demi-heure avant qu'ils se croisent? En
fait, à partir de ce moment là, il leur restera une demi-heure de parcours à
chacun pour arriver à leur croisement; soit 60 km pour l'un et 70 km pour
l'autre; au total: 60 + 70 = 130 km. |
|
|
|
|
Problème Deux
trains partent de deux gares éloignées. Ils
roulent chacun à une vitesse constante en direction l'un de l'autre. Quand
vont-ils se rejoindre? Comme exemple numérique, on prendra: Vitesse
des deux trains: 75 et 25 km/h, et Distance
entre les deux gares 200 km.
|
|
|
Résolution |
|
|
|
Résolution directe Remarquons
que lorsque les deux trains se rencontrent. |
||
|
Ils
ont, à eux deux, parcouru toute la distance entre les deux gares. |
200
km |
|
|
C'est
un peu comme s'ils avaient ajouté leur vitesse pour exécuter plus vite ce
parcours. |
75
+ 25 = 100 km/h |
|
|
|
200
/ 100 = 2 heures |
|
|
Le
premier a parcouru: |
2
x 75 = 150 km |
|
|
Le
second lui a fait: |
2
x 25 = 50 km |
|
|
Nous
utiliserons la formule et le diagramme de temps donnés en rappel ci-dessus. |
||
|
Exprimons
la distance parcourue par le train 1 et par le train 2. D
étant la distance entre les deux gares. |
l1
= v1
. t1 l2
= D – v2
. t2 |
|
|
Au
moment de la rencontre, les trains sont à la même distance au même moment. |
l1 = l2 = l t1 = t2 = t |
|
|
|
l
= v1
. t l
= D – v2
. t |
|
|
L'égalité
en l permet de calculer t. |
v1 . t = D – v2 . t |
|
|
En
exprimant par rapport à t. |
|
|
|
Application numérique |
t = |
D v1
+ v2 |
|
|
= |
200 75
+ 25 |
|
|
= |
2
heures |
|
|
l = |
v1 . t |
|
|
= |
75
x 2 = 150 km |
|
|
||
|
Problème Si
l’on augmente la vitesse d’un train de 30 km/h, on gagne 1 heure sur le
trajet. En
revanche, si l’on diminue la vitesse de 30 km/h, on perd deux heures. Quelle
est la longueur du trajet ? |
Pistes de solution Un
raisonnement intuitif n'est pas très praticable. La
géométrie pourrait sans doute aboutir à la solution. Nous
allons recourir à la géométrie analytique (coordonnées cartésiennes). |
|
|
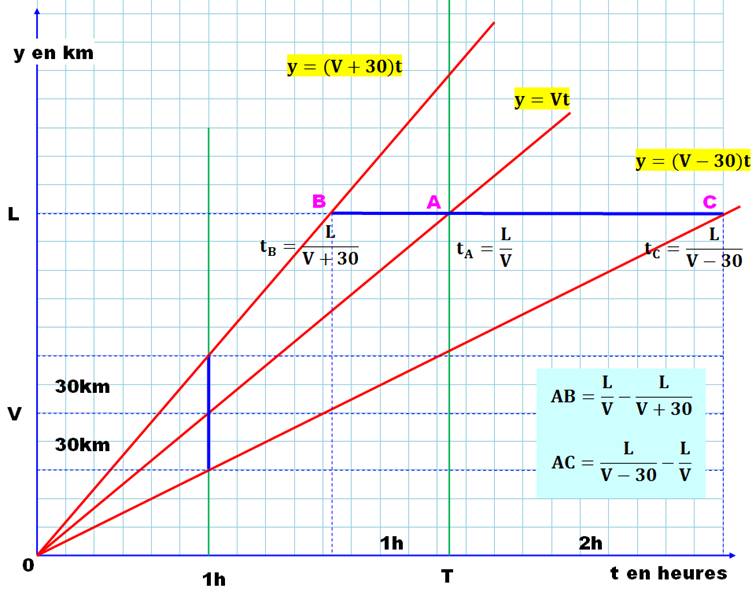
Graphique La
distance y en kilomètres en fonction du temps t. Système de coordonnées en y
et t. On
place le point A à la distance L à parcourir en un temps T (L et T sont
inconnus). Avec
une abscisse à 1 heure, on indique les informations de vitesse V, V + 30 et V
– 30). Ce qui permet de dessiner les droites (rouges) distance en fonction du
temps dans les trois cas. Pour
la distance L, on matérialise les intersections B et C avec les trois
droites. L'écart de temps AB = 1h et AC = 2h.
Résolution |
||
|
OB OC |
y = V . t y = (V + 30) t y = (V – 30) t |
|
|
Abscisse
du point A, profitant que ces trois points ont la même ordonnée y = L. |
|
|
|
Distance
entre ces points dont on sait qu'elles représentent 1 h et 2 h. |
|
|
|
Même
dénominateur |
|
|
|
Calculs
qui donnent un système d'équations à
deux inconnues |
30L
= V² + 30V 30L =
2V² – 60V |
|
|
La
seconde moins la première |
0 =
V² – 90V = V(V – 90) |
|
|
Solution,
outre V = 0 |
V = 90 km/h |
|
|
Longueur
L du trajet: |
L
= (90² + 30 x 90) /30 = 360 km |
|
Merci à
Thibaut C.
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |