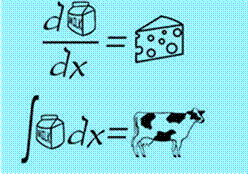|
Édition du: 23/04/2023 |
|
INDEX |
Analyse – Dérivée |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Intérêt et Applications des dérivées (et du calcul différentiel) La dérivée et son extension au calcul différentiel ont été inventées
au milieu du XVIIe siècle. Elles offrent des applications omniprésentes dans
notre monde moderne. On les retrouve partout où il y a quelque chose qui
bouge, qui s'agite, qui transite. Il s'agit d'un outil puissant permettant la modélisation des
phénomènes en perpétuelle animation comme le mouvement des planètes ou, par
exemple, le comportement complexe de la toupie en rotation. |
||
|
|
Sommaire de cette page >>> Introduction >>> Invention de la dérivée >>> Exemples d'application de la dérivée >>> Intérêt de la dérivée >>> Intérêt par domaines d'application |
Débutants Glossaire |
|
J'escalade
la montagne et je constante ma performance: je grimpe de 50 mètres toutes les
heures. |
En
maths, on dit que la dérivée est de 50 m par heure. |
||
|
Je
constate également que je dois avancer de 100 mètres pour monter de 50
mètres. |
C'est
encore une dérivée que nous appelons plus classiquement la pente
et on l'exprime généralement par un pourcentage: 50/100 = 50%. |
||
|
Je
vends des tee-shirts: avant-hier 8 sont partis, hier 10, et aujourd'hui 12.
Un écart de 2 par jour. |
En
maths, on dit que la dérivée est de 2 par jour. |
||
|
Je
roule en voiture sur l'autoroute à 125 km/h. Ce qui veut dire que toutes les
heures je parcours 125 km. |
En
maths, on dit que la dérivée est de 125 kilomètres par heure. La
vitesse
est la dérivée de la distance parcourue par unité de temps. |
||
|
Je
double cette voiture trop lente pour moi. Ma vitesse augmente de 125 à 130
km/h en 5 secondes. Soit 1km/h à chaque seconde. |
Même
la vitesse (qui est une dérivée) peut être, elle-aussi, dérivée. C'est une accélération. Ici, elle
vaut 1km/h/s. |
||
|
La
dérivée est un terme général qui désigne notamment la variation de quelque
chose par unité de temps. |
En
maths, on est encore plus général pour dire que la dérivée qualifie le taux
de variation d'une grandeur par rapport à une autre (pas nécessairement le
temps). |
||
|
Des
mots de la famille de dérivée: |
Taux
de variation, Pente,
Tangente,
Gradient,
Vitesse,
Accélération |
||
|
Des
mots pour calcul avec des dérivées |
Analyse,
Calcul
différentiel, Calcul
intégral. Dérivée
(simple), dérivée seconde (comme l'accélération). |
||
|
On
sait que le carré de 5 est 25 et inversement la
racine carrée de 25 est 5. La même chose existe entre dérivée et intégrale. Exemple:
connaissant la vitesse, il est possible de calculer la distance parcourue;
c'est un calcul intégral |
Le
calcul avec les dérivées cherche à connaitre les variations de grandeurs alors
que le calcul intégral cherche à retrouver les grandeurs à partir des variations
|
||
|
Humour En
dérivant (transformant) le lait peut-on
obtenir du fromage ? En
intégrant (en connaissant) le lait peut-on
remonter à la vache ? |
|
||
|
L'invention
est due à Newton
(1665, alors âgé de 24 ans) qui cherchait à modéliser le mouvement des
planètes. Il lui fallait définir leur orbite à partir de la connaissance de
petites variations. Comment s'y prendre ? Pour
calculer la force exercée par la Terre sur la Lune, faut-il
prendre le centre des astres ou alors chaque particule des astres ? Dans
ce derniers cas il faut ajouter toutes les contributions. C'est l'objet du
calcul intégral qui est une manière d'ajouter un nombre infini de quantités
infinitésimales. Newton
inventa ce calcul en 1666, il proclama alors que son esprit était prêt pour
l'invention de l'attraction universelle – Cette vision est plus proche de la
réalité que celle de la "pomme". |
Il
se trouve que Leibniz,
le contemporain de Newton, faisait la même découverte. Imaginez
la querelle
entre les deux hommes pour en obtenir la paternité ! En
fait, nous avons gardé la méthode de Newton et les simplifications (et
notations) de Leibniz. Cette
branche des mathématiques, nommée Analyse
(calculus en anglais), a été affinée par Cauchy
en introduisant la notion de limite. |
||
|
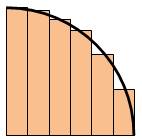
On
savait, comme Archimède, faire des sommes de
tranches approximatives pour calculer une aire. S = S1 + S2 + S3 + … = Σ Si
|
Quelle
est la révolution introduite par Newton et Leibniz ? Ils
ont trouvé le moyen de rendre les tranches aussi fines que possible ! Leur
outil est représenté non plus par une somme de tranches (Σ) mais par ce nouveau symbole (∫) qui induit
une idée de sommation continue.
|
||
|
Le
monde physique comme, par exemple, le monde économique, ne sont pas statique. Dés
qu'il a du mouvement, des variations, les dérivées et les intégrales sont
sollicitées. |
Analyse C'est
la branche des mathématiques qui traite explicitement de la notion de limite,
que ce soit la limite d'une suite ou la limite d'une fonction. Elle inclut
également des notions comme la continuité, la dérivation et l'intégration. Ces
notions sont étudiées dans le contexte des nombres réels ou des nombres
complexes. |
||
|
Le
dérivé a une myriade d'applications scientifiques. L'exemple
classique est évidemment le déplacement et la vitesse. Appelons la fonction
de déplacement s(t) : la variable indépendante est le temps et la variable
dépendante est le déplacement. Supposons
qu'un objet se déplace sur une grande distance en une courte période de
temps, il est évidemment rapide ; s'il se déplace pendant ce même temps sur
une très petite distance, sa vitesse est faible. |
Par
conséquent, nous pouvons voir que la vitesse est une mesure de la sensibilité
de la fonction de déplacement à un changement de temps. Alors,
nous disons: V = dL / dT Les
petits "d" signifie que nous travaillons avec de petites quantités, des quantités qui
s'approchent de zéro. |
||
|
Il
y a de nombreux exemples de la dérivée en science aussi. Par
exemple, en physique nous savons que le champ
électrique peut être défini comme la vitesse à laquelle le potentiel
électrique change. Si,
par exemple, dans une petite zone, le changement de potentiel électrique est
énorme, le champ électrique est fort. |
En
d'autres termes, le champ électrique est la mesure de la sensibilité de la
fonction de potentiel électrique à un changement de distance. Alors,
nous disons: E = dV / dx |
||
|
La
dérivée peut également être utilisée à de nombreuses autres fins, telles que
l'analyse du comportement croissant / décroissant et de la concavité d'une
fonction. |
En
démographie,
la dérivée sert à étudier les variations de population |
||
|
L'outil
dérivation, tellement efficace, n'a pas cessé d'être perfectionné pour
aboutir à ce qui est appelé le calcul différentiel. |
La
dynamique mécanique (étude des objets en mouvements, en translation ou en
rotation, est un immense domaine d'applications. Le
jeune étudiant en études supérieures apprendra à modéliser le mouvement
complexe de la toupie et ses trois modes de comportement: rotation, nutation
et précession. Notions,
évidemment, applicables aux planètes. |
||
|
Le
calcul différentiel a des utilisations en physique, en chimie, en biologie, en
économie, en mathématiques pures, dans toutes les branches de l'ingénierie,
etc. |
Il
n'est pas exagéré de dire que la perspicacité de Newton et de Leibniz dans le
développement du calcul différentiel a véritablement révolutionné notre
capacité à poursuivre de nouvelles branches de la science et de l'ingénierie.
|
||
|
Il
y a beaucoup de choses qui entrent dans l'utilisation du calcul, et il y a
des industries entières qui en dépendent très fortement. Par
exemple, tout secteur qui utilise des graphes
et leurs analyses pour connaitre les tendances et les changements utilisera très
certainement le calcul différentiel d'une manière ou d'une autre. |
L'ingénierie
est un secteur qui utilise beaucoup ce type calcul. Des modèles mathématiques
doivent souvent être créés pour aider à diverses formes de planification
technique. Même
chose pour l'industrie médicale. Tout
ce qui concerne l'étude des mouvements mouvement, comme le développement de
véhicules, l'acoustique, la lumière et l'électricité, utilisera également
beaucoup le calcul différentiel car il est incroyablement utile pour analyser
toute quantité qui change avec le temps. Il
est donc clair qu'il existe de nombreuses industries et activités qui ont
besoin de calcul pour fonctionner correctement. Cela
fait peut-être près de 350 ans que l'idée a été inventée et développée, mais
son importance et sa vitalité n'ont pas diminué depuis qu'elle a été
inventée. |
||
|
Il
existe également des domaines de physique avancée qui se sont appuyés sur
l'utilisation du calcul différentiel pour faire d'autres percées. Dans de
nombreux cas, une théorie et une découverte peuvent servir de point de départ
à d'autres qui viennent après. Par
exemple, Albert Einstein
n'aurait pas été en mesure de concevoir sa célèbre et révolutionnaire théorie de la
relativité sans le calcul différentiel. La
relativité concerne la façon dont l'espace et le temps changent l'un par
rapport à l'autre et, par conséquent, le calcul est au cœur de la théorie. |
D'une
manière générale, le calcul est souvent utilisé lors de la collecte et de
l'analyse des données. C'est
le cas pour les sciences sociales qui font largement appel aux calculs
différentiels. Par
exemple, le calcul de tendances telles que les taux de natalité et de
mortalité ne serait pas possible sans l'utilisation du calcul différentiel. De
même, les prévisions économiques utilisent intensément le calcul différentiel.
|
||
|
Notre
monde technologique fonctionnerait de manière très différente si nous ne
disposions pas du calcul différentiel et d'autres concepts mathématiques
associés pour expliquer et prédire les observations physiques. |
Avec
l'invention du calcul différentiel, l'influence de Newton et Leibniz sur le
monde est sans limite. |
||
|
Conception des structures L'une
des applications les plus critiques du calcul différentiel dans la vie réelle
est l'ingénierie des structures (bâtiments, tours, ponts, etc.). Ce
type de calcul est utilisé pour calculer la résistance, la stabilité, les pertes de chaleur, les exigences
sismiques, etc. Les
architectes utilisent ce type de calcul pour déterminer la quantité optimale
de matériaux nécessaires à la construction de systèmes de soutien capables de
résister à des contraintes sur de longues périodes. Même
des monuments remarquables comme la Tour Eiffel ont été construits en
utilisant le calcul différentiel, notamment pour prédire l'impact de la
résistance au vent. |
|
|
Ingénierie civile des ponts Lors
de la conception des ponts, les ingénieurs doivent prendre en compte trois
éléments structurels : les poutres, les éléments de tension et de
compression. Le calcul permet de déterminer la force agissant sur la poutre
en tenant compte du poids des piétons, du poids des véhicules et du volume de
trafic prévu sur le pont. Sur la base de ces facteurs, les matériaux, la
taille et la capacité peuvent être calculés. |
|
|
Conception électrique Le
calcul intégral et différentiel est crucial pour calculer la tension ou le
courant à travers un circuit électrique notamment dans les condensateurs et
les bobines où la tension met un certain temps à s'établir (variation
exponentielle). Le
calcul intégral est également important dans le calcul de la longueur exacte
d'un câble d'alimentation nécessaire pour connecter des sous-stations
distantes de plusieurs kilomètres. |
|
|
Conception mécanique L'ingénierie
mécanique est un autre grand exemple d'applications. La
pompe utilisée pour remplir un réservoir, les outils de jardinage, les
voitures, les motos, les robots et de nombreux appareils ménagers sont conçus
selon les principes du calcul
différentiel. |
|
|
Industrie spatiale Avant
de lancer une fusée ou une sonde d'exploration de l'espace, les ingénieurs
doivent calculer les forces gravitationnelles du soleil et de la lune pour
savoir comment lancer une sonde ou atteindre la vitesse nécessaire pour se
mettre en orbite autour de la Terre. |
|
|
Médecine Les
applications du calcul dans le domaine médical sont nombreuses : Croissance
bactérienne : les biologistes utilisent le calcul différentiel pour calculer
le taux exact de croissance bactérienne dans une culture en faisant varier
les facteurs environnementaux tels que la température et la source de
nourriture. Diagnostic
des patients : le calcul est crucial dans les tests médicaux utilisés pour
mesurer le débit cardiaque, le flux sanguin et la croissance des tumeurs. Ces
données sont nécessaires pour évaluer correctement l'état de santé d'un patient.
Épidémiologie
: les épidémiologistes qui mènent des recherches sur les maladies
infectieuses utilisent le calcul pour déterminer le taux de propagation et la
zone où une infection est susceptible de se produire. Le calcul peut
également contribuer à l'élaboration d'un plan d'endiguement et à la
recherche de la source d'une infection.
Le
cancer : le calcul est utilisé pour déterminer la croissance ou le
rétrécissement et le nombre de cellules d'une tumeur cancéreuse. En utilisant
une fonction exponentielle, les oncologues analysent la progression ou la
régression d'une maladie. |
|
|
Contrôle chirurgical des globules rouges Le
sang du corps humain est constitué de globules rouges. Lors d'une
intervention chirurgicale, le volume sanguin du patient doit être maintenu
par l'injection d'une solution saline qui se mélange rapidement au sang et se
dilue avec le temps. Le calcul est utilisé pour calculer le volume des
globules rouges afin de pouvoir administrer au patient la quantité adéquate
de solution saline pendant l'opération. Les
cardiologues utilisent le calcul différentiel pour comprendre la dynamique du
flux sanguin nécessaire à la construction d'un modèle d'aorte artificielle
afin de s'assurer qu'elle est placée correctement lors d'une
transplantation. Pharmacologie Il
est essentiel de comprendre la sensibilité aux médicaments pour trouver le
dosage adéquat afin de maximiser l'intégration des médicaments. Les effets
secondaires d'un médicament, provoqués par des facteurs tels que le
changement de température corporelle, peuvent être calculés grâce au calcul
intégral. Les
pharmacologues utilisent le calcul intégral pour déterminer les niveaux de
créatinine dans le sang et évaluer la santé du rein. Ces résultats permettent
de déterminer la posologie des médicaments à administrer. Neurologie La
neurologie est l'étude du système nerveux humain, un réseau très complexe de neurones
qui transmettent les signaux du cerveau à
l'ensemble du corps et contrôlent toutes les activités physiques. Le système
se compose du système nerveux central, du cerveau et de la moelle épinière. Le
calcul intégral est utilisé pour calculer la tension d'un neurone en un point
donné. Et, le calcul différentiel est utilisé pour calculer la variation de
la tension d'un neurone en fonction du temps. Entomologie L'entomologie
est l'étude des insectes.
Un entomologiste mène des recherches, classe les insectes en fonction des
espèces et trouve des solutions sûres pour lutter contre les infestations
d'insectes dans les environnements intérieurs et extérieurs. Le
calcul aux dérivées partielles est utilisé pour modéliser et générer l'activité
des insectes. |
|
|
L'entreprise Les
entreprises modernes bénéficient également de l'application du calcul
différentiel. Voici quelques-unes de ses utilisations : Paiements
par carte de crédit : le calcul est utilisé pour fixer les structures de
paiement et le montant minimum dû par la société de carte de crédit en tenant
compte de variables telles que les taux d'intérêt et la fluctuation du solde.
Économie
: l'élasticité de l'offre et de la demande par rapport au prix est déterminée
à l'aide du calcul différentiel. Les économistes utilisent des variables
telles que la courbe de l'offre et de la demande pour trouver la mesure
exacte de l'élasticité à un point particulier en fonction des changements de
prix. |
|
|
La musique Vous
serez peut-être surpris d'apprendre que l'utilisation du calcul ne se limite
pas à l'ingénierie ou aux sciences médicales, mais qu'elle peut également
s'appliquer à la musique. Voici quelques exemples d'applications : Harmoniques
: une oscillation créée par une harmonique amortie n'est pas infinie, car le
frottement et la résistance de l'air dissipent l'énergie. Le calcul est
utilisé pour anticiper ces mouvements afin d'effectuer les ajustements
appropriés et d'offrir la meilleure expérience musicale aux auditeurs. Acoustique
: la résonance et l'oscillation forcée peuvent être calculées à l'aide du
calcul. La résistance de l'air varie à différentes fréquences et résonne dans
un espace clos lorsqu'un instrument de musique est joué. Grâce au calcul,
nous pouvons améliorer l'acoustique et l'expérience de l'auditeur. |
|
|
Recherche analytique L'application
du calcul à la recherche et au développement a ouvert la voie à une
croissance exponentielle de l'industrie manufacturière, de la gestion des
données, des jeux et d'autres secteurs de services. Ces applications sont,
par exemple, les suivantes : Variables
dans la fabrication : les analystes de recherche utilisent le calcul en
observant différents processus. Sur la base des données collectées, les
entreprises peuvent optimiser leur production, leur productivité et leur
efficacité, ce qui améliore la qualité et les revenus de l'industrie. Évaluer
les données résultant d'enquête : les statisticiens utilisent les données
d'enquête pour trouver un éventail de réponses à différentes questions.
L'utilisation du calcul leur permet de faire des prédictions précises, ce qui
facilite leur processus de prise de décision. Calcul
des taux de natalité et de mortalité : les écologistes utilisent le calcul
pour créer des modèles de population dynamiques qui illustrent la croissance
sans aucune contrainte environnementale. Grâce au calcul, il est possible de
faire des prévisions précises sur l'évolution de la population en tenant
compte des taux de natalité et de mortalité.
Simulation
pour les jeux vidéo : les graphistes utilisent le calcul pour comprendre les
modèles 3D créés dans des conditions changeantes. Sur la base des résultats dérivés du
calcul, les jeux vidéo et les films d'animation sont réalisés dans une
perspective de monde réel. |
|
|
Météorologie La
compréhension des modèles météorologiques est essentielle pour l'agriculture,
les alertes météorologiques et la préparation en cas de conditions extrêmes. Calcul
des modèles météorologiques : les météorologues utilisent des équations de
calcul différentiel pour prévoir les effets des différentes conditions
météorologiques sur l'atmosphère en ce qui concerne les changements de
température, d'humidité et de pression. Le
domaine de la prévision météorologique est d'ailleurs une activité très
gourmande en puissance de calcul. L'atmosphère est découpée en "cubes",
des mailles de quelques centaines de mètres de côté. Ce sont les données de
chacune d'elles qui sont analysées pour prévoir le temps. C'est d'ailleurs en
météorologie que l'on rencontre les plus gros ordinateurs du monde. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |