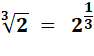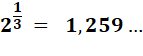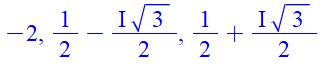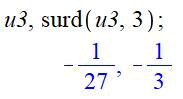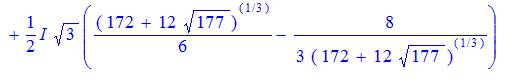NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 05/02/2019

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                      Brèves de Maths

      

ÉQUATIONS

 

Débutants

Équations

Troisième degré

 

Glossaire

Équations

 

 

INDEX

Équations

 

Théorie

Exemple 1

Méthode

Historique

Factorisation

Exemple 2

Exemple 3

 

Sommaire de cette page

>>> Notations

>>> Exemple:    x3 + x² – x + 2 = 0

>>> Exemple:    x3 + x² – x – 2 = 0

>>> Autour de cette équation

 

 

 

ÉQUATIONS du 3e degré

Exemple de résolution

 

x3 + x² – x + 2  = 0

 

Pour les personnes impatientes, allez directement à la méthode de calcul "bestiale".

 

 

Notations

 

Sur cette page, on remplace les racines par des puissances fractionnaires.

Note: cette astuce peut vous être utile si vous utilisez une calculette avec la fonction yx.

 

 

Pour faciliter le suivi des opérations, on calcule les valeurs au fur et à mesure

Voir Formules de résolution de l'équation du 3e degré

 

 

Exemple 1

CALCUL des COEFFICIENTS

x3 + ax² + bx + c = 0

x3 +   x²  –   x +  2 = 0

a

b

c

=   1

= – 1

=   2

 

p = b – a²/3

 

p

= –1 – 1/3

= – 4/3

= – 1,333…

 

q = a/27 (2a² – 9b) + c

q

= 1/27 (2 + 9) + 2

= 11/27 + 2

= 2,407…

 

 

CALCUL de L'EXPRESSION SOUS RACINE CARRÉE

(q/2)² + (p/3)3

(q/2)²

= ( 2,407… / 2 )²

= 1,448…

 

 

(p/3)3

= (– 1,333… / 3 )3

= – 0,0877…

 

 

Somme

Racine

= 1,3603

= 1,166… = 17/15

 

CALCUL de U et V

u3 = -q/2 + Racine

u3

 

u

= –2,407... / 2 + 1,166…

= –0,0375...

= –0,333... = -1/3

 

v3 = -q/2 - Racine

v3

 

v

= –2,407... / 2 – 1,166…

= –2,369...

= –1,333... = -4/3

 

 

CALCUL de x1, x2 & x3

x1 =

 

 

 

u + v – 1/3

–0,333... – 1,333... – 0,333...

– 2, 000...

 

x2 =

 

 

 

{ – u/2 – v/2 – 1/3 }

0,333/2 + 1,333/2 – 0,333
0, 5

+ ½ i 3 { u – v }

+ ½ i 3 (–0,333 + 1,333)

+ 0, 866 i

x3 =

0, 5

– 0, 866 i

Résumé

Note 0,866… = 3 / 2

 

Racine cubique avec Maple

Pour obtenir la racine réelle, utilisez l'instruction surd.

Si u3 = -1 /27, l'instruction surd calcule sa racine cubique réelle =>

Voir Exemple de résolution complète avec Maple

 

 

 

Exemple 2 – La même avec changement de signe

CALCUL des COEFFICIENTS

x3 + ax² + bx + c = 0

x3 +   x²  –    x –  2 = 0

a

b

c

=  1

= –1

= –2

 

p = b – a²/3

 

p

= –1 – 1/3

= – 4/3

= – 1,333…

 

q = a/27 (2a² – 9b) + c

q

= 1/27 (2 + 9) – 2

= 11/27 – 2

= – 1,592…

 

 

CALCUL de L'EXPRESSION SOUS RACINE CARRÉE

(q/2)² + (p/3)3

(q/2)²

= ( –1,592… / 2 )²

= 0,633…

 

 

(p/3)3

= (– 1,333… / 3 )3

= – 0,0877…

 

 

Somme

Racine

= 0,546…

= 0,739…

 

CALCUL de U et V

u3 = –q/2 + Racine

u3

 

u

= 1,592… / 2 + 0,739…

= 1,535…

= 1,153…

 

v3 = –q/2 – Racine

v3

 

v

= 1,592… / 2 – 0,739…

= 0,057…

= 0,385…

 

 

CALCUL de x1, x2 & x3

x1 =

u + v – 1/3

1,15 + 0,38 – 0,333

1, 205

1, 2055694304005903117 …

 

 

x2 =

{ – u/2 – v/2 – 1/3 }

– 1,153/2 – 0,385/2 – 0333
– 1,102

–1, 1027847152002951558 …

 

+ ½ i 3 { u – v }

+ ½ i 3 (1,153 – 0,385)

+ 0, 665 i

+ 0, 66545695115281347665 i

 

x3 =

– 1,102

= –1, 1027847152002951558 …

 

– 0, 665 i

–  0, 66545695115281347665 i

 

 

En conservant les radicaux, on trouverait ces valeurs littérales

 

x3 + x² – x – 2 = 0

 

 

 

AUTOUR DE CETTE ÉQUATION

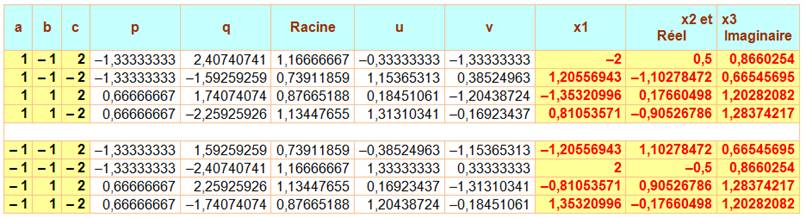
Solution pour toutes les combinaisons de signes pour a, b et c

 

Programmation sur tableur

 

 

a

b

c

d

e

f

g

h

1

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

3

a

b

c

p

q

racine

u

v

4

1

–1

2

=B4–A4*A4/3

=A4/27*(2*A4*A4–9*B4)+C4

=RACINE((E4/2)^2+(D4/3)^3)

=(–E4/2+F4)^(1/3)

=(–E4/2–F4)^(1/3)

 

i

j

k

 

 

 

 

 

 

x1

Reel

Imaginaire

=G4+H4–A4/3

=–G4/2–H4/2–A4/3

=RACINE(3)*(G4–H4)/2

Voir méthode sur tableur avec un copier–coller direct

 

 

 

Suite

*    Autres exemples du 3e degré

*    Autres pages sur 3e degré

Voir

*    Algorithme d'Héron

*    Équation de Pell

*    Méthode de Newton

*    Système d'équations particulier

Cette page

http://villemin.gerard.free.fr/ThNbDemo/Eqa3dex.htm